NESTML dopamine-modulated STDP synapse tutorial
Some text in this this notebook is copied verbatim from [1]. Network diagrams were modeled after [2].
Pavlov and Thompson (1902) first described classical conditioning: a phenomenon in which a biologically potent stimulus–the Unconditional Stimulus (UC)—is initially paired with a neutral stimulus—the Conditional Stimulus (CS). After many trials, learning is observed when the previously neutral stimuli start to elicit a response similar to that which was previously only elicited by the biologically potent stimulus. Pavlov and Thompson performed many experiments with dogs, observing their response (by monitoring salivation) to the appearance of a person who has been feeding them and the actual food appearing (UC). He demonstrated that the dogs started to salivate in the presence of the person who has been feeding them (or any other CS), rather than just when the food appears, because the CS had previously been associated with food.
Image credits: https://www.psychologicalscience.org/observer/revisiting-pavlovian-conditioning
In this tutorial, a dopamine-modulated STDP model is created in NESTML, and we characterize the model before using it in a network (reinforcement) learning task.
Model
Izhikevich (2007) revisits an important question: how does an animal know which of the many cues and actions preceding a reward should be credited for the reward? Izhikevich explains that dopamine-modulated STDP has a built-in instrumental conditioning property, i.e., the associations between cues, actions and rewards are learned automatically by reinforcing the firing patterns (networks of synapses) responsible, even when the firings of those patterns are followed by a delayed reward or masked by other network activity.
To achieve this, each synapse has an eligibility trace \(C\):
where \(\tau_C\) is the decay time constant of the eligibility trace and \(\text{STDP}(\Delta t)\) represents the magnitude of the change to make to the eligibility trace in response to a pair of pre- and post-synaptic spikes with temporal difference \(\Delta t = t_\text{post} − t_\text{pre}\). (This is just the usual STDP rule, see https://nestml.readthedocs.io/en/latest/tutorials/stdp_windows/stdp_windows.html.) Finally, \(\delta(t − t_\text{pre/post})\) is a Dirac delta function used to apply the effect of STDP to the trace at the times of pre- or post-synaptic spikes.
The concentration of dopamine is described by a variable \(D\):
where \(\tau_d\) is the time constant of dopamine re-absorption, \(D_c\) is a real number indicating the increase in dopamine concentration caused by each incoming dopaminergic spike; \(t_d^f\) are the times of these spikes.
Equations (1, 2) are then combined to calculate the change in synaptic strength \(W\):
When a post-synaptic spike arrives very shortly after a pre-synaptic spike, a standard STDP rule would immediately potentiate the synaptic strength. However, when using the three-factor STDP rule, this potentiation would instead be applied to the eligibility trace.
Because changes to the synaptic strength are gated by dopamine concentration \(D\) (Equation 3), changes are only made to the synaptic strength if \(D \neq 0\). Furthermore, if the eligibility trace has decayed back to 0 before any dopaminergic spikes arrive, the synaptic strength will also not be changed.
[1]:
%matplotlib inline
from typing import List, Optional
import matplotlib as mpl
mpl.rcParams['axes.formatter.useoffset'] = False
mpl.rcParams['axes.grid'] = True
mpl.rcParams['grid.color'] = 'k'
mpl.rcParams['grid.linestyle'] = ':'
mpl.rcParams['grid.linewidth'] = 0.5
mpl.rcParams['figure.dpi'] = 120
mpl.rcParams['figure.figsize'] = [8., 3.]
import matplotlib.pyplot as plt
import nest
import numpy as np
import os
import random
import re
from pynestml.codegeneration.nest_code_generator_utils import NESTCodeGeneratorUtils
/home/charl/.local/lib/python3.11/site-packages/matplotlib/projections/__init__.py:63: UserWarning: Unable to import Axes3D. This may be due to multiple versions of Matplotlib being installed (e.g. as a system package and as a pip package). As a result, the 3D projection is not available.
warnings.warn("Unable to import Axes3D. This may be due to multiple versions of "
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
Generating code with NESTML
To generate fast code, NESTML needs to process the synapse model together with the neuron model that will be its postsynaptic partner in the network instantiantion (see https://nestml.readthedocs.io/en/latest/nestml_language/synapses_in_nestml.html#generating-code).
In this tutorial, we will use a very simple integrate-and-fire model, where arriving spikes cause an instantaneous increment of the membrane potential, the “iaf_psc_delta” model.
We first define a helper function to generate the C++ code for the models, build it as a NEST extension module, and load the module into the kernel. The resulting model names are composed of associated neuron and synapse partners, because of the co-generation, for example, “stdp_synapse__with_iaf_psc_delta” and “iaf_psc_delta__with_stdp_synapse”.
Because NEST does not support un- or reloading of modules at the time of writing, we implement a workaround that appends a unique number to the name of each generated model, for example, “stdp_synapse_3cc945f__with_iaf_psc_delta_3cc945f” and “iaf_psc_delta_3cc945f__with_stdp_synapse_3cc945f”.
The resulting neuron and synapse model names are returned by the function, so we do not have to think about these internals.
Formulating the model in NESTML
We now go on to define the full synapse model in NESTML:
[2]:
nestml_stdp_dopa_model = """
model neuromodulated_stdp_synapse:
state:
w real = 1.
n real = 0. # Neuromodulator concentration
c real = 0. # Eligibility trace
pre_tr real = 0.
post_tr real = 0.
parameters:
d ms = 1 ms @nest::delay
tau_tr_pre ms = 20 ms # STDP time constant for weight changes caused by pre-before-post spike pairings.
tau_tr_post ms = 20 ms # STDP time constant for weight changes caused by post-before-pre spike pairings.
tau_c ms = 1000 ms # Time constant of eligibility trace
tau_n ms = 200 ms # Time constant of dopaminergic trace
b real = 0. # Dopaminergic baseline concentration
Wmax real = 200. # Maximal synaptic weight
Wmin real = 0. # Minimal synaptic weight
A_plus real = 1. # Multiplier applied to weight changes caused by pre-before-post spike pairings. If b (dopamine baseline concentration) is zero, then A_plus is simply the multiplier for facilitation (as in the stdp_synapse model). If b is not zero, then A_plus will be the multiplier for facilitation only if n - b is positive, where n is the instantenous dopamine concentration in the volume transmitter. If n - b is negative, A_plus will be the multiplier for depression.
A_minus real = 1.5 # Multiplier applied to weight changes caused by post-before-pre spike pairings. If b (dopamine baseline concentration) is zero, then A_minus is simply the multiplier for depression (as in the stdp_synapse model). If b is not zero, then A_minus will be the multiplier for depression only if n - b is positive, where n is the instantenous dopamine concentration in the volume transmitter. If n - b is negative, A_minus will be the multiplier for facilitation.
A_vt real = 1. # Multiplier applied to dopa spikes
equations:
pre_tr' = -pre_tr / tau_tr_pre
post_tr' = -post_tr / tau_tr_post
internals:
tau_s 1/ms = (tau_c + tau_n) / (tau_c * tau_n)
input:
pre_spikes <- spike
post_spikes <- spike
mod_spikes <- spike
output:
spike
onReceive(mod_spikes):
n += A_vt / tau_n
onReceive(post_spikes):
post_tr += 1.
# facilitation
c += A_plus * pre_tr
onReceive(pre_spikes):
pre_tr += 1.
# depression
c -= A_minus * post_tr
# deliver spike to postsynaptic partner
emit_spike(w, d)
# update from time t to t + resolution()
update:
integrate_odes()
# resolution() returns the timestep to be made (in units of time)
# the sequence here matters: the update step for w requires the "old" values of c and n
w -= c * ( n / tau_s * expm1( -tau_s * resolution() ) \
- b * tau_c * expm1( -resolution() / tau_c ))
w = max(0., w)
c = c * exp(-resolution() / tau_c)
n = n * exp(-resolution() / tau_n)
"""
Generate the code, build the user module and make the model available to instantiate in NEST:
[3]:
# generate and build code
module_name, neuron_model_name, synapse_model_name = NESTCodeGeneratorUtils.generate_code_for("../../../models/neurons/iaf_psc_delta_neuron.nestml",
nestml_stdp_dopa_model,
post_ports=["post_spikes"],
mod_ports=["mod_spikes"],
logging_level="INFO")
[1,GLOBAL, INFO]: List of files that will be processed:
[2,GLOBAL, INFO]: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/iaf_psc_delta_neuron.nestml
[3,GLOBAL, INFO]: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/neuromodulated_stdp_synapse.nestml
[4,GLOBAL, INFO]: Target platform code will be generated in directory: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target'
[5,GLOBAL, INFO]: Target platform code will be installed in directory: '/tmp/nestml_target_2nbwam92'
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
[6,GLOBAL, INFO]: The NEST Simulator version was automatically detected as: master
[7,GLOBAL, INFO]: Given template root path is not an absolute path. Creating the absolute path with default templates directory '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/pynestml/codegeneration/resources_nest/point_neuron'
[8,GLOBAL, INFO]: Given template root path is not an absolute path. Creating the absolute path with default templates directory '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/pynestml/codegeneration/resources_nest/point_neuron'
[9,GLOBAL, INFO]: Given template root path is not an absolute path. Creating the absolute path with default templates directory '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/pynestml/codegeneration/resources_nest/point_neuron'
[10,GLOBAL, INFO]: The NEST Simulator installation path was automatically detected as: /home/charl/julich/nest-simulator-install
[11,GLOBAL, INFO]: Start processing '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/iaf_psc_delta_neuron.nestml'!
[13,iaf_psc_delta_neuron_nestml, INFO, [51:79;51:79]]: Implicit magnitude conversion from pA to pA buffer with factor 1.0
[14,iaf_psc_delta_neuron_nestml, INFO, [51:15;51:74]]: Implicit magnitude conversion from mV / ms to pA / pF with factor 1.0
[15,GLOBAL, INFO]: Start processing '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/neuromodulated_stdp_synapse.nestml'!
[17,neuromodulated_stdp_synapse_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[18,neuromodulated_stdp_synapse_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[19,neuromodulated_stdp_synapse_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[22,neuromodulated_stdp_synapse_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[23,neuromodulated_stdp_synapse_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[24,neuromodulated_stdp_synapse_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[26,iaf_psc_delta_neuron_nestml, INFO, [51:79;51:79]]: Implicit magnitude conversion from pA to pA buffer with factor 1.0
[27,iaf_psc_delta_neuron_nestml, INFO, [51:15;51:74]]: Implicit magnitude conversion from mV / ms to pA / pF with factor 1.0
[29,neuromodulated_stdp_synapse_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[30,neuromodulated_stdp_synapse_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[31,neuromodulated_stdp_synapse_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[32,GLOBAL, INFO]: State variables that will be moved from synapse to neuron: ['post_tr']
[33,GLOBAL, INFO]: Parameters that will be copied from synapse to neuron: ['tau_tr_post']
[34,GLOBAL, INFO]: Moving state var defining equation(s) post_tr
[35,GLOBAL, INFO]: Moving state variables for equation(s) post_tr
[36,GLOBAL, INFO]: Moving definition of post_tr from synapse to neuron
[37,GLOBAL, INFO]: Moving statement post_tr += 1.0
[38,GLOBAL, INFO]: In synapse: replacing ``continuous`` type input ports that are connected to postsynaptic neuron with suffixed external variable references
[39,GLOBAL, INFO]: Copying parameters from synapse to neuron...
[40,GLOBAL, INFO]: Copying definition of tau_tr_post from synapse to neuron
[41,GLOBAL, INFO]: Adding suffix to variables in spike updates
[42,GLOBAL, INFO]: In synapse: replacing variables with suffixed external variable references
[43,GLOBAL, INFO]: • Replacing variable post_tr
[44,GLOBAL, INFO]: ASTSimpleExpression replacement made (var = post_tr__for_neuromodulated_stdp_synapse_nestml) in expression: A_minus * post_tr
[47,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[48,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[49,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
INFO:Analysing input:
INFO:{
"dynamics": [
{
"expression": "V_m' = (-(V_m - E_L)) / tau_m + 0 * (1.0 / 1.0) + (I_e + I_stim) / C_m",
"initial_values": {
"V_m": "E_L"
}
}
],
"options": {
"output_timestep_symbol": "__h"
},
"parameters": {
"C_m": "250",
"E_L": "(-70)",
"I_e": "0",
"V_min": "(-oo) * 1",
"V_reset": "(-70)",
"V_th": "(-55)",
"refr_T": "2",
"tau_m": "10",
"tau_syn": "2"
}
}
INFO:Processing global options...
INFO:Processing input shapes...
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + 0 * (1.0 / 1.0) + (I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m
INFO:All known variables: [V_m], all parameters used in ODEs: {tau_m, I_e, C_m, I_stim, E_L}
INFO:No numerical value specified for parameter "I_stim"
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + 0 * (1.0 / 1.0) + (I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m
INFO:Finding analytically solvable equations...
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph.dot
[50,GLOBAL, INFO]: Successfully constructed neuron-synapse pair iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml, neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml
[51,GLOBAL, INFO]: Analysing/transforming model 'iaf_psc_delta_neuron_nestml'
[52,iaf_psc_delta_neuron_nestml, INFO, [43:0;94:0]]: Starts processing of the model 'iaf_psc_delta_neuron_nestml'
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable_before_propagated.dot
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable.dot
INFO:Generating propagators for the following symbols: V_m
INFO:update_expr[V_m] = -E_L*__P__V_m__V_m + E_L + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
INFO:In ode-toolbox: returning outdict =
INFO:[
{
"initial_values": {
"V_m": "E_L"
},
"parameters": {
"C_m": "250.000000000000",
"E_L": "-70.0000000000000",
"I_e": "0",
"tau_m": "10.0000000000000"
},
"propagators": {
"__P__V_m__V_m": "exp(-__h/tau_m)"
},
"solver": "analytical",
"state_variables": [
"V_m"
],
"update_expressions": {
"V_m": "-E_L*__P__V_m__V_m + E_L + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m"
}
}
]
INFO:Analysing input:
INFO:{
"dynamics": [
{
"expression": "V_m' = (-(V_m - E_L)) / tau_m + 0 * (1.0 / 1.0) + (I_e + I_stim) / C_m",
"initial_values": {
"V_m": "E_L"
}
},
{
"expression": "post_tr__for_neuromodulated_stdp_synapse_nestml' = (-post_tr__for_neuromodulated_stdp_synapse_nestml) / tau_tr_post__for_neuromodulated_stdp_synapse_nestml",
"initial_values": {
"post_tr__for_neuromodulated_stdp_synapse_nestml": "0.0"
}
}
],
"options": {
"output_timestep_symbol": "__h"
},
"parameters": {
"C_m": "250",
"E_L": "(-70)",
"I_e": "0",
"V_min": "(-oo) * 1",
"V_reset": "(-70)",
"V_th": "(-55)",
"refr_T": "2",
"tau_m": "10",
"tau_syn": "2",
"tau_tr_post__for_neuromodulated_stdp_synapse_nestml": "20"
}
}
INFO:Processing global options...
INFO:Processing input shapes...
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + 0 * (1.0 / 1.0) + (I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m
INFO:
Processing differential-equation form shape post_tr__for_neuromodulated_stdp_synapse_nestml with defining expression = "(-post_tr__for_neuromodulated_stdp_synapse_nestml) / tau_tr_post__for_neuromodulated_stdp_synapse_nestml"
INFO: Returning shape: Shape "post_tr__for_neuromodulated_stdp_synapse_nestml" of order 1
INFO:Shape post_tr__for_neuromodulated_stdp_synapse_nestml: reconstituting expression -post_tr__for_neuromodulated_stdp_synapse_nestml/tau_tr_post__for_neuromodulated_stdp_synapse_nestml
INFO:All known variables: [V_m, post_tr__for_neuromodulated_stdp_synapse_nestml], all parameters used in ODEs: {tau_m, I_e, C_m, I_stim, E_L, tau_tr_post__for_neuromodulated_stdp_synapse_nestml}
INFO:No numerical value specified for parameter "I_stim"
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + 0 * (1.0 / 1.0) + (I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:
Processing differential-equation form shape post_tr__for_neuromodulated_stdp_synapse_nestml with defining expression = "(-post_tr__for_neuromodulated_stdp_synapse_nestml) / tau_tr_post__for_neuromodulated_stdp_synapse_nestml"
INFO: Returning shape: Shape "post_tr__for_neuromodulated_stdp_synapse_nestml" of order 1
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m
INFO:Shape post_tr__for_neuromodulated_stdp_synapse_nestml: reconstituting expression -post_tr__for_neuromodulated_stdp_synapse_nestml/tau_tr_post__for_neuromodulated_stdp_synapse_nestml
INFO:Finding analytically solvable equations...
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph.dot
[54,GLOBAL, INFO]: Analysing/transforming model 'iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml'
[55,iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml, INFO, [43:0;94:0]]: Starts processing of the model 'iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml'
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m
INFO:Shape post_tr__for_neuromodulated_stdp_synapse_nestml: reconstituting expression -post_tr__for_neuromodulated_stdp_synapse_nestml/tau_tr_post__for_neuromodulated_stdp_synapse_nestml
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable_before_propagated.dot
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable.dot
INFO:Generating propagators for the following symbols: V_m, post_tr__for_neuromodulated_stdp_synapse_nestml
INFO:update_expr[V_m] = -E_L*__P__V_m__V_m + E_L + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m
INFO:update_expr[post_tr__for_neuromodulated_stdp_synapse_nestml] = __P__post_tr__for_neuromodulated_stdp_synapse_nestml__post_tr__for_neuromodulated_stdp_synapse_nestml*post_tr__for_neuromodulated_stdp_synapse_nestml
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
WARNING:Not preserving expression for variable "post_tr__for_neuromodulated_stdp_synapse_nestml" as it is solved by propagator solver
INFO:In ode-toolbox: returning outdict =
INFO:[
{
"initial_values": {
"V_m": "E_L",
"post_tr__for_neuromodulated_stdp_synapse_nestml": "0.0"
},
"parameters": {
"C_m": "250.000000000000",
"E_L": "-70.0000000000000",
"I_e": "0",
"tau_m": "10.0000000000000",
"tau_tr_post__for_neuromodulated_stdp_synapse_nestml": "20.0000000000000"
},
"propagators": {
"__P__V_m__V_m": "exp(-__h/tau_m)",
"__P__post_tr__for_neuromodulated_stdp_synapse_nestml__post_tr__for_neuromodulated_stdp_synapse_nestml": "exp(-__h/tau_tr_post__for_neuromodulated_stdp_synapse_nestml)"
},
"solver": "analytical",
"state_variables": [
"V_m",
"post_tr__for_neuromodulated_stdp_synapse_nestml"
],
"update_expressions": {
"V_m": "-E_L*__P__V_m__V_m + E_L + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m",
"post_tr__for_neuromodulated_stdp_synapse_nestml": "__P__post_tr__for_neuromodulated_stdp_synapse_nestml__post_tr__for_neuromodulated_stdp_synapse_nestml*post_tr__for_neuromodulated_stdp_synapse_nestml"
}
}
]
INFO:Analysing input:
INFO:{
"dynamics": [
{
"expression": "pre_tr' = (-pre_tr) / tau_tr_pre",
"initial_values": {
"pre_tr": "0.0"
}
}
],
"options": {
"output_timestep_symbol": "__h"
},
"parameters": {
"A_minus": "1.5",
"A_plus": "1.0",
"A_vt": "1.0",
"Wmax": "200.0",
"Wmin": "0.0",
"b": "0.0",
"d": "1",
"tau_c": "1000",
"tau_n": "200",
"tau_tr_post": "20",
"tau_tr_pre": "20"
}
}
INFO:Processing global options...
INFO:Processing input shapes...
INFO:
Processing differential-equation form shape pre_tr with defining expression = "(-pre_tr) / tau_tr_pre"
INFO: Returning shape: Shape "pre_tr" of order 1
INFO:Shape pre_tr: reconstituting expression -pre_tr/tau_tr_pre
INFO:All known variables: [pre_tr], all parameters used in ODEs: {tau_tr_pre}
INFO:
Processing differential-equation form shape pre_tr with defining expression = "(-pre_tr) / tau_tr_pre"
INFO: Returning shape: Shape "pre_tr" of order 1
INFO:Shape pre_tr: reconstituting expression -pre_tr/tau_tr_pre
INFO:Finding analytically solvable equations...
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph.dot
INFO:Shape pre_tr: reconstituting expression -pre_tr/tau_tr_pre
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable_before_propagated.dot
[57,GLOBAL, INFO]: Analysing/transforming synapse neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.
[58,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [2:0;66:0]]: Starts processing of the model 'neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml'
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable.dot
INFO:Generating propagators for the following symbols: pre_tr
INFO:update_expr[pre_tr] = __P__pre_tr__pre_tr*pre_tr
WARNING:Not preserving expression for variable "pre_tr" as it is solved by propagator solver
INFO:In ode-toolbox: returning outdict =
INFO:[
{
"initial_values": {
"pre_tr": "0.0"
},
"parameters": {
"tau_tr_pre": "20.0000000000000"
},
"propagators": {
"__P__pre_tr__pre_tr": "exp(-__h/tau_tr_pre)"
},
"solver": "analytical",
"state_variables": [
"pre_tr"
],
"update_expressions": {
"pre_tr": "__P__pre_tr__pre_tr*pre_tr"
}
}
]
[60,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[61,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[62,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[64,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[65,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[66,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[67,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.cpp
[68,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.h
[69,iaf_psc_delta_neuron_nestml, INFO, [43:0;94:0]]: Successfully generated code for the model: 'iaf_psc_delta_neuron_nestml' in: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
[70,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp
[71,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.h
[72,iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml, INFO, [43:0;94:0]]: Successfully generated code for the model: 'iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml' in: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
Generating code for the synapse neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.
[73,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h
[74,neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml, INFO, [2:0;66:0]]: Successfully generated code for the model: 'neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml' in: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
[75,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module.cpp
[76,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module.h
[77,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/CMakeLists.txt
[78,GLOBAL, INFO]: Successfully generated NEST module code in '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
CMake Warning (dev) at CMakeLists.txt:95 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
nestml_9557cf48dd76469a8f5dc4ea86b34c42_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'nestml_9557cf48dd76469a8f5dc4ea86b34c42_module' using
make
make install
The library file libnestml_9557cf48dd76469a8f5dc4ea86b34c42_module.so will be installed to
/tmp/nestml_target_2nbwam92
The module can be loaded into NEST using
(nestml_9557cf48dd76469a8f5dc4ea86b34c42_module) Install (in SLI)
nest.Install(nestml_9557cf48dd76469a8f5dc4ea86b34c42_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target
[ 25%] Building CXX object CMakeFiles/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module_module.dir/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module.o
[ 50%] Building CXX object CMakeFiles/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module_module.dir/iaf_psc_delta_neuron_nestml.o
[ 75%] Building CXX object CMakeFiles/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module_module.dir/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp: In member function ‘void iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp:183:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
183 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp: In member function ‘virtual void iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp:287:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
287 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp:282:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
282 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.cpp: In member function ‘void iaf_psc_delta_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.cpp:173:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
173 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_delta_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.cpp:266:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
266 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_delta_neuron_nestml.cpp:261:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
261 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
In file included from /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module.cpp:36:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierPtrRport>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:62:5: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:671:106: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:862:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
862 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::recompute_internal_variables() [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:876:3: required from ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierPtrRport]’
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierPtrRport>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:62:5: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:671:106: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:849:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
849 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:103:34: required from ‘void nest::ModelManager::register_specific_connection_model_(const std::string&) [with CompleteConnecionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:67:80: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:671:106: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:862:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
862 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::recompute_internal_variables() [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:876:3: required from ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierIndex]’
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:103:34: required from ‘void nest::ModelManager::register_specific_connection_model_(const std::string&) [with CompleteConnecionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:67:80: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:671:106: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:849:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
849 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:589:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
589 | auto get_t = [_tr_t](){ return _tr_t; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:614:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
614 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:649:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
649 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:517:18: warning: unused variable ‘__resolution’ [-Wunused-variable]
517 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:519:10: warning: variable ‘get_thread’ set but not used [-Wunused-but-set-variable]
519 | auto get_thread = [tid]()
| ^~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::trigger_update_weight(size_t, const std::vector<nest::spikecounter>&, double, const CommonPropertiesType&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int; CommonPropertiesType = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:446:38: required from ‘void nest::Connector<ConnectionT>::trigger_update_weight(long int, size_t, const std::vector<nest::spikecounter>&, double, const std::vector<nest::ConnectorModel*>&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:433:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:1009:18: warning: unused variable ‘_tr_t’ [-Wunused-variable]
1009 | const double _tr_t = start->t_;
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:991:10: warning: unused variable ‘timestep’ [-Wunused-variable]
991 | double timestep = 0;
| ^~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:589:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
589 | auto get_t = [_tr_t](){ return _tr_t; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:614:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
614 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:649:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
649 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:517:18: warning: unused variable ‘__resolution’ [-Wunused-variable]
517 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:519:10: warning: variable ‘get_thread’ set but not used [-Wunused-but-set-variable]
519 | auto get_thread = [tid]()
| ^~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::trigger_update_weight(size_t, const std::vector<nest::spikecounter>&, double, const CommonPropertiesType&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int; CommonPropertiesType = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:446:38: required from ‘void nest::Connector<ConnectionT>::trigger_update_weight(long int, size_t, const std::vector<nest::spikecounter>&, double, const std::vector<nest::ConnectorModel*>&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:433:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:1009:18: warning: unused variable ‘_tr_t’ [-Wunused-variable]
1009 | const double _tr_t = start->t_;
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:991:10: warning: unused variable ‘timestep’ [-Wunused-variable]
991 | double timestep = 0;
| ^~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::process_mod_spikes_spikes_(const std::vector<nest::spikecounter>&, double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:563:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:699:12: warning: unused variable ‘cd’ [-Wunused-variable]
699 | double cd;
| ^~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::update_internal_state_(double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:584:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:935:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
935 | auto get_t = [t_start](){ return t_start; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::process_mod_spikes_spikes_(const std::vector<nest::spikecounter>&, double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:563:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:699:12: warning: unused variable ‘cd’ [-Wunused-variable]
699 | double cd;
| ^~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::update_internal_state_(double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:584:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_delta_neuron_nestml.h:935:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
935 | auto get_t = [t_start](){ return t_start; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
[100%] Linking CXX shared module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module.so
[100%] Built target nestml_9557cf48dd76469a8f5dc4ea86b34c42_module_module
[100%] Built target nestml_9557cf48dd76469a8f5dc4ea86b34c42_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_2nbwam92/nestml_9557cf48dd76469a8f5dc4ea86b34c42_module.so
Running the simulation in NEST
Let’s define a function that will instantiate a simple network with one presynaptic cell and one postsynaptic cell connected by a single synapse, then run a simulation and plot the results.
[4]:
def run_network(pre_spike_time, post_spike_time, vt_spike_times,
neuron_model_name,
synapse_model_name,
resolution=.1, # [ms]
delay=1., # [ms]
lmbda=1E-6,
sim_time=None, # if None, computed from pre and post spike times
synapse_parameters=None, # optional dictionary passed to the synapse
fname_snip="",
debug=False):
#nest.set_verbosity("M_WARNING")
nest.set_verbosity("M_ALL")
nest.ResetKernel()
nest.Install(module_name)
nest.SetKernelStatus({'resolution': resolution})
# create spike_generators with these times
pre_sg = nest.Create("spike_generator",
params={"spike_times": [pre_spike_time]})
post_sg = nest.Create("spike_generator",
params={"spike_times": [post_spike_time]})
vt_sg = nest.Create("spike_generator",
params={"spike_times": vt_spike_times})
# create volume transmitter
vt = nest.Create("volume_transmitter")
vt_parrot = nest.Create("parrot_neuron")
nest.Connect(vt_sg, vt_parrot)
nest.Connect(vt_parrot, vt, syn_spec={"synapse_model": "static_synapse",
"weight": 1.,
"delay": 1.}) # delay is ignored!
# set up custom synapse models
wr = nest.Create('weight_recorder')
nest.CopyModel(synapse_model_name, "stdp_nestml_rec",
{"weight_recorder": wr[0],
"w": 1.,
"delay": delay,
"receptor_type": 0,
"volume_transmitter": vt,
"tau_tr_pre": 10.,
})
# create parrot neurons and connect spike_generators
pre_neuron = nest.Create("parrot_neuron")
post_neuron = nest.Create(neuron_model_name)
spikedet_pre = nest.Create("spike_recorder")
spikedet_post = nest.Create("spike_recorder")
spikedet_vt = nest.Create("spike_recorder")
#mm = nest.Create("multimeter", params={"record_from" : ["V_m"]})
nest.Connect(pre_sg, pre_neuron, "one_to_one", syn_spec={"delay": 1.})
nest.Connect(post_sg, post_neuron, "one_to_one", syn_spec={"delay": 1., "weight": 9999.})
nest.Connect(pre_neuron, post_neuron, "all_to_all", syn_spec={'synapse_model': 'stdp_nestml_rec'})
#nest.Connect(mm, post_neuron)
nest.Connect(pre_neuron, spikedet_pre)
nest.Connect(post_neuron, spikedet_post)
nest.Connect(vt_parrot, spikedet_vt)
# get STDP synapse and weight before protocol
syn = nest.GetConnections(source=pre_neuron, synapse_model="stdp_nestml_rec")
if synapse_parameters is None:
synapse_parameters = {}
nest.SetStatus(syn, synapse_parameters)
initial_weight = nest.GetStatus(syn)[0]["w"]
np.testing.assert_allclose(initial_weight, 1)
nest.Simulate(sim_time)
updated_weight = nest.GetStatus(syn)[0]["w"]
actual_t_pre_sp = nest.GetStatus(spikedet_pre)[0]["events"]["times"][0]
actual_t_post_sp = nest.GetStatus(spikedet_post)[0]["events"]["times"][0]
pre_spike_times_ = nest.GetStatus(spikedet_pre, "events")[0]["times"]
assert len(pre_spike_times_) == 1 and pre_spike_times_[0] > 0
post_spike_times_ = nest.GetStatus(spikedet_post, "events")[0]["times"]
assert len(post_spike_times_) == 1 and post_spike_times_[0] > 0
vt_spike_times_ = nest.GetStatus(spikedet_vt, "events")[0]["times"]
assert len(vt_spike_times_) == 1 and vt_spike_times_[0] > 0
#dt = actual_t_post_sp - actual_t_pre_sp
dt = 0.
dw = updated_weight
return dt, dw
[5]:
def run_vt_spike_timing_experiment(neuron_model_name, synapse_model_name, synapse_parameters=None):
sim_time = 10000. # [ms] -- make sure to simulate for much longer than the eligibility trace
# time constant, which is typically the slowest time constant in
# the system, PLUS the time of the latest vt spike
pre_spike_time = 1. # [ms]
post_spike_time = 3. # [ms]
delay = .5 # dendritic delay [ms]
dt_vec = []
dw_vec = []
for vt_spike_time in np.round(np.linspace(4, 5000, 12)).astype(float): # sim_time - 10 * delay
dt, dw = run_network(pre_spike_time, post_spike_time, [vt_spike_time],
neuron_model_name,
synapse_model_name,
delay=delay, # [ms]
synapse_parameters=synapse_parameters,
sim_time=sim_time)
dt_vec.append(vt_spike_time)
dw_vec.append(dw)
return dt_vec, dw_vec, delay
[6]:
fig, ax = plt.subplots()
for A_vt in [1., -1.]:
dt_vec, dw_vec, delay = run_vt_spike_timing_experiment(neuron_model_name,
synapse_model_name,
synapse_parameters={"A_vt": A_vt})
ax.plot(dt_vec, dw_vec, marker='o', label="$A_{vt}$ = " + str(A_vt))
ax.set_xlabel("Time of dopa spike [ms]")
ax.set_ylabel("Weight at $t = \infty$")
ax.legend()
Apr 19 11:33:12 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:12 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:12 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:12 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:12 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:12 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:12 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:12 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:12 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:12 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:13 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:13 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:13 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:14 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:14 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:14 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:14 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:14 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:14 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:14 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:14 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:14 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:14 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:14 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:14 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:14 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:14 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
Apr 19 11:33:14 NodeManager::prepare_nodes [Info]:
Preparing 11 nodes for simulation.
Apr 19 11:33:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 11
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:14 SimulationManager::run [Info]:
Simulation finished.
[6]:
<matplotlib.legend.Legend at 0x7fb610f89010>
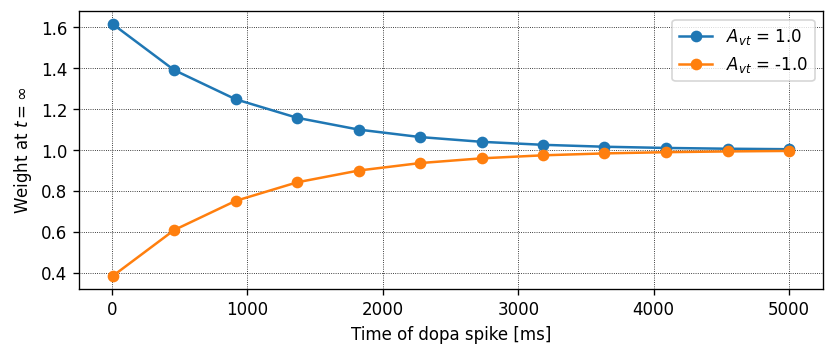
Learning through dopamine
In this section we simulate the spiking activity of a group of neurons with the learning rule as described above. Here, we perform the simulation on 10 iaf_psc_delta neurons in which each of the neurons receives input from an independent Poisson source of 50Hz. These neurons are also connected to a single dopamine spike source. These dopamine spikes are delivered to the neurons as reward and punishment signals at specific time intervals.
Single dopamine source, multiple independent pre-post cell pairs (3 pairs shown).
[7]:
# Labels for x and y axes for traces used in plotting functions
labels = {"c": {"x_label": "Times [ms]", "y_label": "Eligibility \ntrace (c)"},
"w": {"x_label": "Times [ms]", "y_label": "Weight \ntrace (w)"},
"pre_tr": {"x_label": "Times [ms]", "y_label": "Presynaptic \ntrace (pre_tr)"},
"n": {"x_label": "Times [ms]", "y_label": "Doapmine \ntrace (n)"}
}
[8]:
# Plot trace values for a neurons or set of neurons
def plot_traces_for_neuron(log, recordables, neuron_numbers=None, pos_dopa_spike_times=None, neg_dopa_spike_times=None):
"""
Plots the trace values for the given list of neuron IDs
"""
times = log["t"]
trace_values = {}
# Initialize the list if "neuron_numbers" is None, which corresponds to all neurons
if neuron_numbers is None:
neuron_numbers = np.array([i+1 for i in range(10)])
# The actual neuron numbers are -1 of the given numbers
neuron_numbers_actual = np.array(neuron_numbers) - 1
# Get the values of recordables for the given neuron IDs
for recordable in recordables:
trace_values[recordable] = np.array(log[recordable])[:, neuron_numbers_actual]
n_neurons = len(neuron_numbers)
palette = plt.get_cmap('tab10')
for i in range(n_neurons):
fig, ax = plt.subplots(nrows=len(recordables), sharex=True, squeeze=False)
ax = ax.flatten()
fig.suptitle("Trace values for Neuron " + str(neuron_numbers[i]))
for j, recordable in enumerate(recordables):
ax[j].plot(times, trace_values[recordable][:, i], label="neuron " + str(neuron_numbers[i]), color=palette(neuron_numbers_actual[i]))
ax[j].set_xlim(xmin=0)
ax[j].set_ylabel(labels[recordable]["y_label"], rotation=0, ha="right", va="center")
ax[j].legend(loc="upper right", labelspacing=0.)
if pos_dopa_spike_times is not None:
ax[j].scatter(pos_dopa_spike_times, np.ones_like(pos_dopa_spike_times) * np.amin(trace_values[recordable][:, i]), marker="^", c="green", s=20)
if neg_dopa_spike_times is not None:
ax[j].scatter(neg_dopa_spike_times, np.ones_like(neg_dopa_spike_times) * np.amin(trace_values[recordable][:, i]), marker="^", c="red", s=20)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
[9]:
def plot_spiking_activity(neuron_spike_times, pos_dopa_spike_times, neg_dopa_spike_times, source_ids, total_t_sim):
fig, ax = plt.subplots()
palette = plt.get_cmap('tab10')
n_neurons = len(neuron_spike_times)
y_ticks = [i * 10 for i in range(n_neurons, 0, -1)]
for i in range(n_neurons):
ax.scatter(neuron_spike_times[i], np.ones_like(neuron_spike_times[i]) * y_ticks[i], color=palette(i), s=1)
if pos_dopa_spike_times is not None:
ax.scatter(pos_dopa_spike_times, np.zeros_like(pos_dopa_spike_times), marker="^", c="green", s=100)
if neg_dopa_spike_times is not None:
ax.scatter(neg_dopa_spike_times, np.zeros_like(pos_dopa_spike_times), marker="^", c="red", s=100)
ax.set_xlim(0., total_t_sim)
ax.set_ylim(ymin=0)
ax.set_xlim(xmin=0)
ax.set_yticks(y_ticks)
ax.set_yticklabels(source_ids)
ax.set_xlabel("Time [ms]")
ax.set_ylabel("Neuron ID")
plt.tight_layout()
fig.show()
Here, we setup the network with 10 neurons each connected to a Poisson source. The neurons are also connected to a volume transmitter that acts as a dopamine spike source.
[10]:
# simulation parameters
resolution = .1
# network parameters
n_neurons = 10
tau_n = 50.
tau_c = 100.
pre_poisson_rate = 50. # [s^-1]
initial_weight = 5.6 # controls initial firing rate before potentiation
# stimulus parameters
pos_dopa_spike_times = [2000, 3000, 4000]
neg_dopa_spike_times = [8000, 9000, 10000]
A_vt = [10., -10.]
nest.set_verbosity("M_ALL")
nest.ResetKernel()
nest.Install(module_name)
nest.SetKernelStatus({'resolution': resolution})
# Create the neurons
neurons = nest.Create(neuron_model_name, n_neurons)
# Create a poisson generator
poisson_gen = nest.Create("poisson_generator", n_neurons, params={"rate": pre_poisson_rate})
parrot_neurons = nest.Create("parrot_neuron", n_neurons)
# Spike generators
vt_sg = nest.Create("spike_generator", params={"spike_times": pos_dopa_spike_times + neg_dopa_spike_times})
# Spike recorder
spike_rec = nest.Create("spike_recorder")
spike_rec_vt = nest.Create("spike_recorder")
spike_re_pt = nest.Create("spike_recorder")
# create volume transmitter
vt = nest.Create("volume_transmitter")
vt_parrot = nest.Create("parrot_neuron")
nest.Connect(vt_sg, vt_parrot, syn_spec={"weight": -1.})
nest.Connect(vt_parrot, vt, syn_spec={"synapse_model": "static_synapse",
"weight": 1.,
"delay": 1.})
# multimeters
mms = [nest.Create("multimeter", params= {"record_from": ["V_m"]}) for _ in range(n_neurons)]
# set up custom synapse models
wr = nest.Create('weight_recorder')
nest.CopyModel(synapse_model_name, "stdp_nestml_rec",
{"weight_recorder": wr[0],
"w": initial_weight,
"d": delay,
"receptor_type": 0,
"volume_transmitter": vt,
"tau_n": tau_n,
"tau_c": tau_c,
})
# Connect everything
nest.Connect(poisson_gen, parrot_neurons, "one_to_one")
nest.Connect(parrot_neurons, neurons, "one_to_one", syn_spec="stdp_nestml_rec")
nest.Connect(neurons, spike_rec)
nest.Connect(vt_parrot, spike_rec_vt)
for i in range(n_neurons):
nest.Connect(mms[i], neurons[i])
Apr 19 11:33:15 Install [Info]:
loaded module nestml_9557cf48dd76469a8f5dc4ea86b34c42_module
Apr 19 11:33:15 iaf_psc_delta_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:15 iaf_psc_delta_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:33:15 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
This is a helper function that runs the simulation in chunks of time intervals and records the values of the synapse properties passed as recordables.
[11]:
def run_simulation_in_chunks(sim_chunks, sim_time, recordables, neurons):
sim_time_per_chunk = sim_time / sim_chunks
# Init log to collect the values of all recordables
log = {}
log["t"] = []
# Initialize all the arrays
# Additional one entry is to store the trace value before the simulation begins
for rec in recordables:
log[rec] = (sim_chunks + 1) * [[]]
# Get the value of trace values before the simulation
syn = nest.GetConnections(target=neurons, synapse_model="stdp_nestml_rec")
for rec in recordables:
log[rec][0] = syn.get(rec)
log["t"].append(nest.GetKernelStatus("biological_time"))
# Run the simulation in chunks
nest.Prepare()
for i in range(sim_chunks):
print(str(i) + " out of " + str(sim_chunks))
# Set the reward / punishment for dopa spikes
# Set the punishment signal only when the timed during simulation == the first negative dopa spike time
# Otherwise set the reward signal
sim_start_time = i * sim_time_per_chunk
sim_end_time = sim_start_time + sim_time_per_chunk
if sim_end_time > neg_dopa_spike_times[0]:
syn.set({"A_vt": A_vt[1]})
else:
syn.set({"A_vt": A_vt[0]})
nest.Run(sim_time//sim_chunks)
# log current values
log["t"].append(nest.GetKernelStatus("biological_time"))
# Get the value of trace after the simulation
for rec in recordables:
log[rec][i + 1] = syn.get(rec)
nest.Cleanup()
return log
Run simulation in NEST
Let’s run the simulation and record the neuron spike times and synapse parameters like the eligibility trace c, the presynaptic trace pre_tr, the dopamine trace n, and the weight w.
[12]:
# Run simulation
sim_time = 12000
n_chunks = 400
recordables = ["c", "pre_tr", "n", "w"]
log = run_simulation_in_chunks(n_chunks, sim_time, recordables, neurons)
times = spike_rec.get("events")["times"]
senders = spike_rec.get("events")["senders"]
times_vt = spike_rec_vt.get("events")["times"]
connections = nest.GetConnections(neurons)
source_ids = connections.get("source") # source IDs of all neurons
source_ids = list(set(source_ids))
neuron_spike_times = [[] for _ in range(n_neurons)]
for i in range(n_neurons):
neuron_spike_times[i] = times[senders == source_ids[i]]
0 out of 400
Apr 19 11:33:15 NodeManager::prepare_nodes [Info]:
Preparing 47 nodes for simulation.
1 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
2 out of 400
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
3 out of 400
4 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
5 out of 400
6 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
7 out of 400
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
8 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
9 out of 400
10 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
11 out of 400
12 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
13 out of 400
14 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
15 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
16 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
17 out of 400
18 out of 400
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
19 out of 400
20 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
21 out of 400
22 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
23 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
24 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
25 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
26 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
27 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
28 out of 400
29 out of 400
30 out of 400
31 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
32 out of 400
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 Simulat33 out of 400
34 out of 400
35 out of 400
ionManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
36 out of 400
37 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
38 out of 400
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
39 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
40 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
41 out of 400
42 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
43 out of 400
44 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
45 out of 400
46 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
47 out of 400
48 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
49 out of 400
50 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
51 out of 400
52 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
53 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
54 out of 400
55 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
56 out of 400
57 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
58 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
59 out of 400
60 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
61 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
62 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
63 out of 400
64 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
65 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
66 out of 400
67 out of 400
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
68 out of 400
69 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
70 out of 400
71 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
72 out of 400
73 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
74 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
75 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
76 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
77 out of 400
78 out of 400
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
79 out of 400
80 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
81 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
82 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
83 out of 400
84 out of 400
Apr 19 11:33:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:15 SimulationManager::run [Info]:
Simulation finished.
85 out of 400
86 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
87 out of 400
88 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
89 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
90 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
91 out of 400
92 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
93 out of 400
94 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
95 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
96 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
97 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
98 out of 400
99 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
100 out of 400
101 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
102 out of 400
103 out of 400
104 out of 400
105 out of 400
106 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
107 out of 400
108 out of 400
109 out of 400
110 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 Simulat111 out of 400
ionManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
112 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
113 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
114 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
115 out of 400
116 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
117 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
118 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
119 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
120 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
121 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
122 out of 400
123 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
124 out of 400
125 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
126 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
127 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
128 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
129 out of 400
130 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
131 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
132 out of 400
133 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
134 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
135 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
136 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
137 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
138 out of 400
139 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
140 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
141 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
142 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
143 out of 400
144 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
145 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
146 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
147 out of 400
148 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
149 out of 400
150 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
151 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
152 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
153 out of 400
154 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
155 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
156 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
157 out of 400
158 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
159 out of 400
160 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
161 out of 400
162 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
163 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
164 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
165 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
166 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
167 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
168 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
169 out of 400
170 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
171 out of 400
172 out of 400
173 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
174 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
175 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
176 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
177 out of 400
178 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
179 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
180 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
181 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
182 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
183 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
184 out of 400
185 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
186 out of 400
187 out of 400
188 out of 400
189 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
190 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
191 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
192 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
193 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
194 out of 400
195 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
196 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
197 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
198 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
199 out of 400
200 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
201 out of 400
202 out of 400
203 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
204 out of 400
205 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
206 out of 400
207 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
208 out of 400
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
209 out of 400
210 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
211 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
212 out of 400
213 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
214 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
215 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
216 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
217 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
218 out of 400
219 out of 400
220 out of 400
221 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
222 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
223 out of 400
224 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
225 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
226 out of 400
227 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
228 out of 400
229 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
230 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
231 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
232 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
233 out of 400
234 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
235 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:16 SimulationManager::run [Info]:
Simulation finished.
236 out of 400
Apr 19 11:33:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
237 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
238 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
239 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
240 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
241 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
242 out of 400
243 out of 400
244 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
245 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
246 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
247 out of 400
248 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
249 out of 400
250 out of 400
251 out of 400
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
252 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
253 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
254 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
255 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
256 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
257 out of 400
258 out of 400
259 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
260 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
261 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
262 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
263 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
264 out of 400
265 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
266 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
267 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
268 out of 400
269 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
270 out of 400
271 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
272 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
273 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
274 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
275 out of 400
276 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
277 out of 400
278 out of 400
279 out of 400
280 out of 400
281 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
282 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 Simulat283 out of 400
ionManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
284 out of 400
285 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
286 out of 400
287 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
288 out of 400
289 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
290 out of 400
291 out of 400
292 out of 400
293 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
294 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
295 out of 400
296 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
297 out of 400
298 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
299 out of 400
300 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
301 out of 400
302 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
303 out of 400
304 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
305 out of 400
306 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
307 out of 400
308 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
309 out of 400
310 out of 400
311 out of 400
312 out of 400
313 out of 400
314 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
315 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
316 out of 400
317 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
318 out of 400
319 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
320 out of 400
321 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
322 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
323 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
324 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
325 out of 400
326 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
327 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
328 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
329 out of 400
330 out of 400
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
331 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
332 out of 400
333 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
334 out of 400
335 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
336 out of 400
337 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
338 out of 400
339 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
340 out of 400
341 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
342 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
343 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
344 out of 400
345 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
346 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
347 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
348 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
349 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
350 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
351 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
352 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
353 out of 400
354 out of 400
355 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
356 out of 400
357 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 Simulat358 out of 400
ionManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
359 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
360 out of 400
361 out of 400
362 out of 400
363 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
364 out of 400
365 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
366 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
367 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
368 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
369 out of 400
370 out of 400
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
371 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
372 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
373 out of 400
374 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
375 out of 400
376 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:17 SimulationManager::run [Info]:
Simulation finished.
377 out of 400
Apr 19 11:33:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
378 out of 400
379 out of 400
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
380 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
381 out of 400
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
382 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
383 out of 400
384 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
385 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
386 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
387 out of 400
388 out of 400
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
389 out of 400
390 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
391 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
392 out of 400
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
393 out of 400
394 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
395 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
396 out of 400
397 out of 400
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
398 out of 400
399 out of 400
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:33:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 47
Simulation time (ms): 30
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:33:18 SimulationManager::run [Info]:
Simulation finished.
Spiking activity
[13]:
# Plot the spiking activity
plot_spiking_activity(neuron_spike_times, pos_dopa_spike_times, neg_dopa_spike_times, source_ids, sim_time)
/tmp/ipykernel_335797/2151756254.py:23: UserWarning:FigureCanvasAgg is non-interactive, and thus cannot be shown
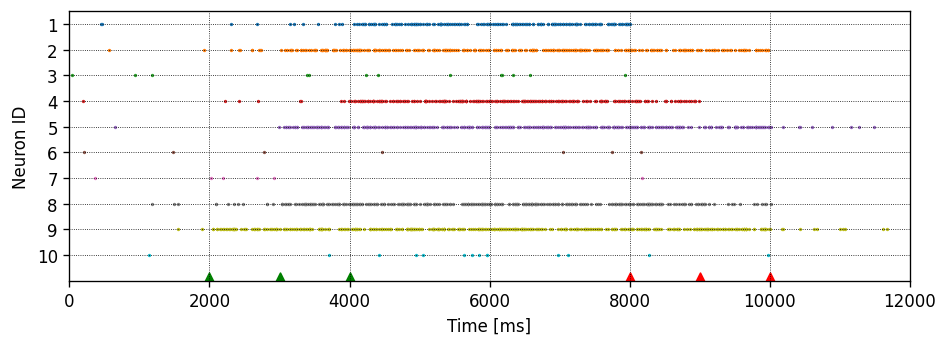
From the spiking activity of the neurons, we can see that the firing rate of the neurons increases after the dopamine spikes or reward signals (green triangles in the plot) are applied to the synapses. Consequently, when the punishment signals are applied (red triangles), the firing rate decreases. In order to understand the dynamics, let’s plot the different trace variables of the synapse.
Plot the trace values
Let’s plot the trace values and the weight for each synapse. Note that the dopamine trace is the same for every synapse.
[14]:
# Plot trace values for all neurons
plot_traces_for_neuron(log, ["c", "w", "n"], pos_dopa_spike_times=pos_dopa_spike_times, neg_dopa_spike_times=neg_dopa_spike_times)
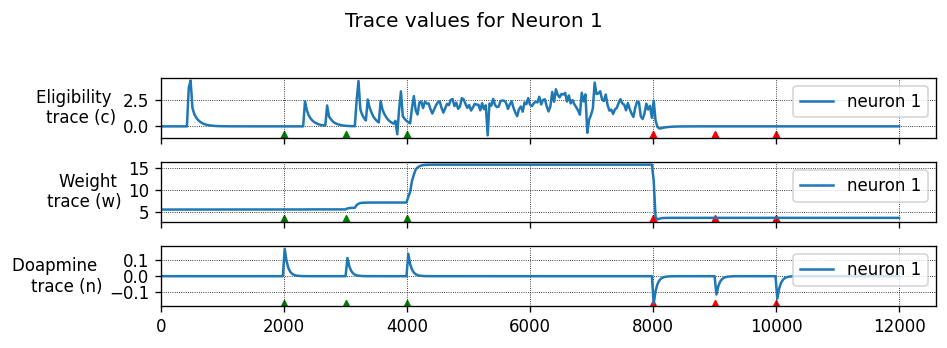
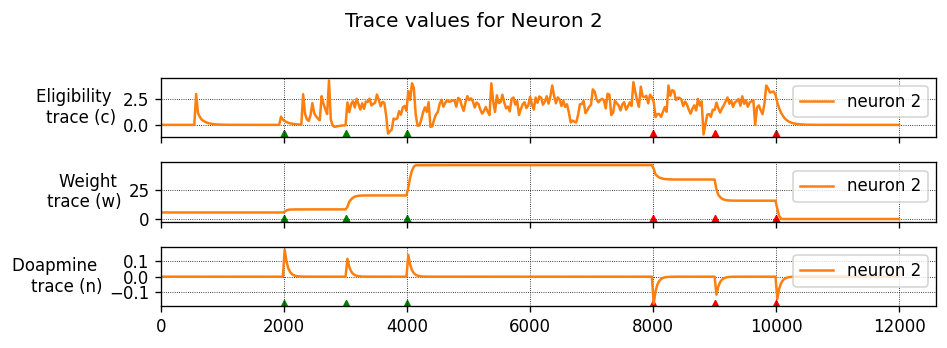
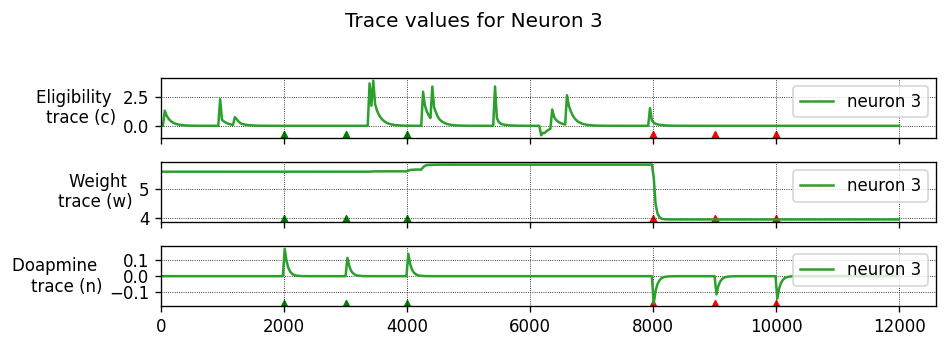
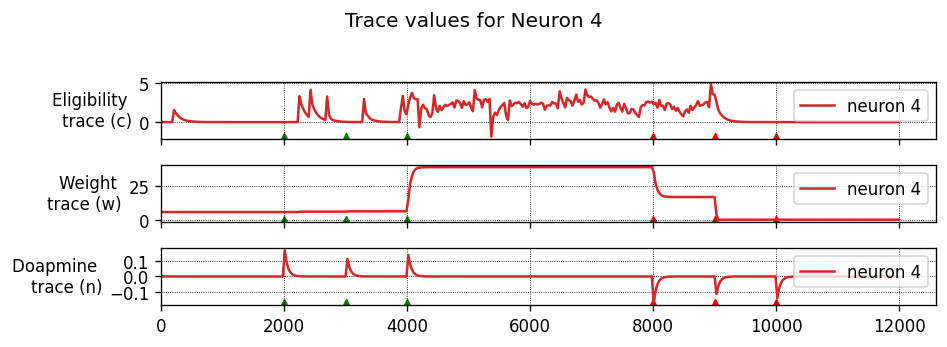
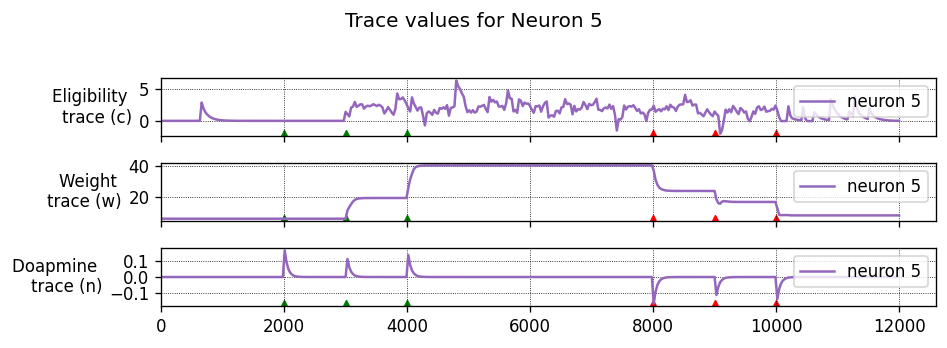
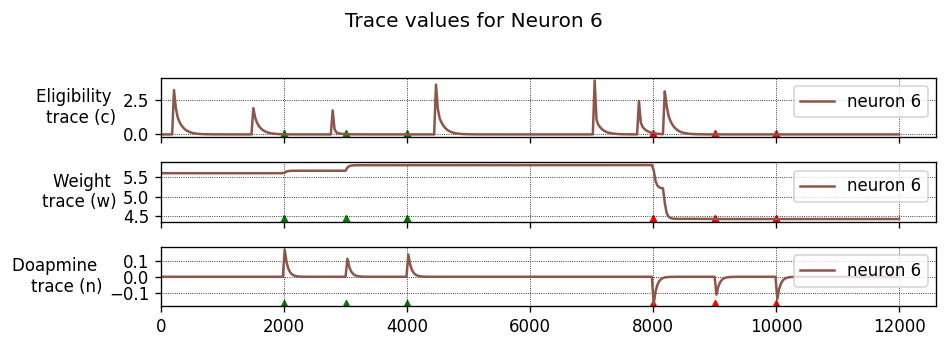
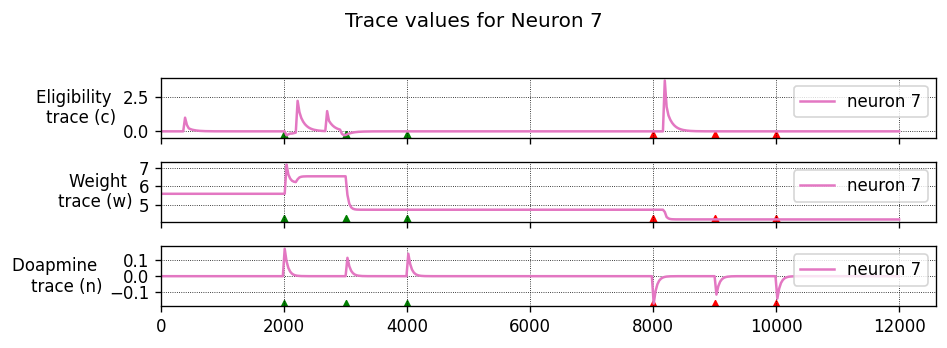
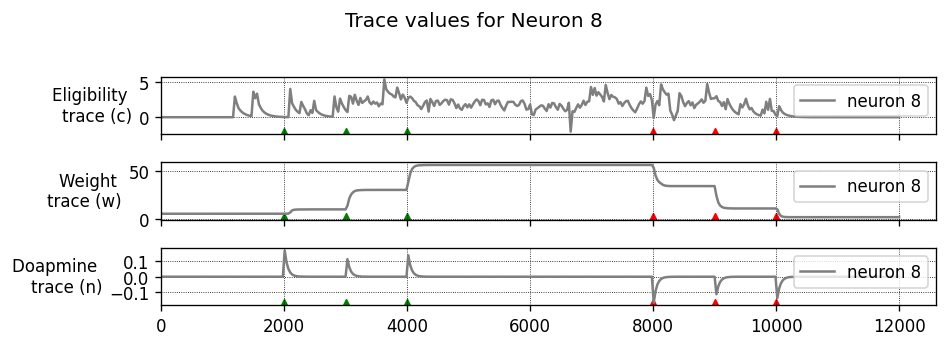
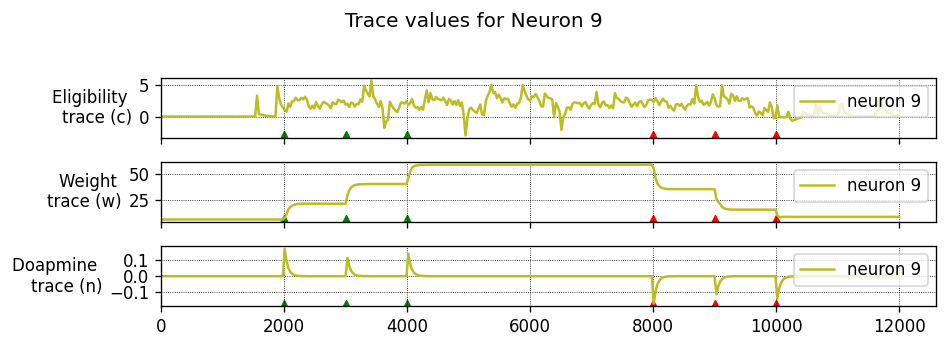
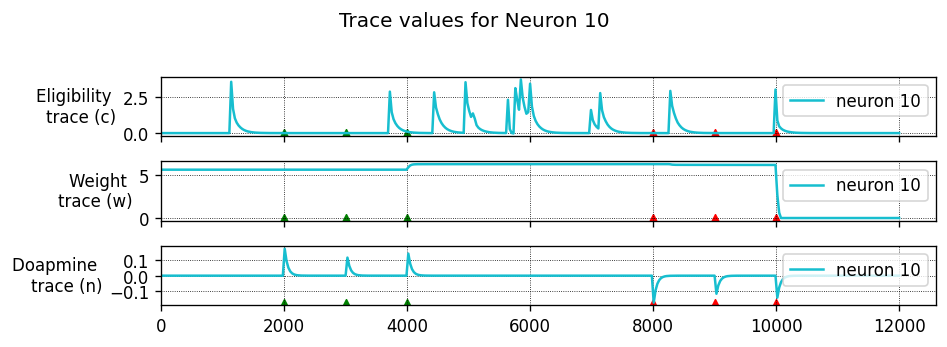
As we can see, the eligibility trace values for neurons 1, 2, 4, 5, and 9 are large when the dopamine spikes are applied, which increases the weights of these neurons, resulting in stronger firing. If the dopamine spikes arrive while the eligibility trace is close to zero, the weight does not increase or increases only very little.
In our simulation above, we set a low value of 50 ms for the time constant of the dopamine trace \(\tau_n\). This means that the dopamine signal does not sustain for a long time, allowing only some neurons that fire around the time when the dopamine spikes (reward signal) are applied have their synapses strengthened (see the weight trace plots) and consequenty increase their firing rate. Similarly, the firing rate is decreased when the dopamine spikes (punishment signals) are applied. For neuron 9, the punishment signal doesn’t seem to affect the firing rate. This behavior can be explained by the time constant of the signals and the very large weights after the initial potentiation, resulting in sustained firing.
Play around with the initial weight value w and dopamine time constant \(\tau_n\) to simulate and see the effects of these values on firing rates and trace values.
Noisy Cue-Association: Temporal Credit-Assignment Task
In this experiment, the synapse is embedded in a network consisting of 800 excitatory, and 200 inhibitory neurons, that are randomly and sparsely connected. The network is in the balanced state, meaning that excitatory currents are roughly matched in mean amplitude over time, and the neurons have a membrane potential close to the firing threshold, firing only sparsely and with statistics approaching that of a Poisson process [4].
Using this network, we illustrate a classical (Pavlovian) conditioning experiment: rewarding a conditioned stimulus \(S_1\) embedded in a continuous stream of irrelevant but equally salient stimuli [3]. The conditioned stimulus is repeatedly presented to the network, causing a transient of activity against the background of low-rate random background firing. The CS is always followed by a reward, which reinforces the recurrent excitatory pathways in the network.
To simulate the experiment, n_subgroups random sets of neurons (each representing stimulus \(S_1\) through \(S_\text{n\_subgroups}\)) are chosen from the pool of excitatory and inhibitory neurons in the network. To present a stimulus to the network, we create n_subgroups spike generators (named stim_sg), and connect each to its individual target group of subgroup_size neurons in the network (here, 50) with a very large weight, so that the stimulus spike generator firing
will cause all of the neurons in the subgroup to fire.
A continuous input stream is generated, consisting of stimuli \(S_i (1 \leq i \leq \text{n\_subgroups})\) in a random order with random intervals of rate stimulus_rate and at least min_stimulus_presentation_delay. After every presentation of the CS (\(S_1\)), a reward in the form of an increase of extra-cellular dopamine is delivered to all plastic synapses in the network, after a random delay between min_dopa_reinforcement_delay and max_dopa_reinforcement_delay. These
delays were chosen lower than in the original publications ([1], [3]) to keep the simulation times low for this interactive tutorial. The delay is large enough to allow irrelevant input stimuli to be presented during the waiting period; these can be considered as distractors.
At the beginning of the experiment the neurons representing each stimulus \(S_i\) respond equally. However, after many trials, the network starts to show reinforced response to the CS (\(S_1\)). Because synapses coming out of neurons representing \(S_1\) are always tagged with the eligibility trace when the reward is delivered, whereas the synapses connected to neurons representing irrelevant stimuli will only be occasionally tagged, the average strength of synaptic connections from neurons representing stimulus \(S_1\) becomes stronger than the mean synaptic connection strength in the rest of the network. Therefore, the other neurons in the network learn to listen more closely to the stimulus \(S_1\), because the activation of this pathway causes a reward.
This network uses neurons with a decaying-exponential shaped postsynaptic current. Let’s first generate the code for those.
[15]:
# generate and build code
module_name, neuron_model_name, synapse_model_name = NESTCodeGeneratorUtils.generate_code_for("../../../models/neurons/iaf_psc_exp_neuron.nestml",
nestml_stdp_dopa_model,
post_ports=["post_spikes"],
mod_ports=["mod_spikes"],
logging_level="INFO")
[1,GLOBAL, INFO]: List of files that will be processed:
[2,GLOBAL, INFO]: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/iaf_psc_exp_neuron.nestml
[3,GLOBAL, INFO]: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/neuromodulated_stdp_synapse.nestml
[4,GLOBAL, INFO]: Target platform code will be generated in directory: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target'
[5,GLOBAL, INFO]: Target platform code will be installed in directory: '/tmp/nestml_target_nxqmze5r'
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
[6,GLOBAL, INFO]: The NEST Simulator version was automatically detected as: master
[7,GLOBAL, INFO]: Given template root path is not an absolute path. Creating the absolute path with default templates directory '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/pynestml/codegeneration/resources_nest/point_neuron'
[8,GLOBAL, INFO]: Given template root path is not an absolute path. Creating the absolute path with default templates directory '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/pynestml/codegeneration/resources_nest/point_neuron'
[9,GLOBAL, INFO]: Given template root path is not an absolute path. Creating the absolute path with default templates directory '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/pynestml/codegeneration/resources_nest/point_neuron'
[10,GLOBAL, INFO]: The NEST Simulator installation path was automatically detected as: /home/charl/julich/nest-simulator-install
[11,GLOBAL, INFO]: Start processing '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/iaf_psc_exp_neuron.nestml'!
[13,iaf_psc_exp_neuron_nestml, INFO, [67:39;67:63]]: Implicit magnitude conversion from pA to pA buffer with factor 1.0
[14,iaf_psc_exp_neuron_nestml, INFO, [67:15;67:30]]: Implicit magnitude conversion from mV / ms to pA / pF with factor 1.0
[15,GLOBAL, INFO]: Start processing '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/neuromodulated_stdp_synapse.nestml'!
[17,neuromodulated_stdp_synapse_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[18,neuromodulated_stdp_synapse_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[19,neuromodulated_stdp_synapse_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[22,neuromodulated_stdp_synapse_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[23,neuromodulated_stdp_synapse_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[24,neuromodulated_stdp_synapse_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[26,iaf_psc_exp_neuron_nestml, INFO, [67:39;67:63]]: Implicit magnitude conversion from pA to pA buffer with factor 1.0
[27,iaf_psc_exp_neuron_nestml, INFO, [67:15;67:30]]: Implicit magnitude conversion from mV / ms to pA / pF with factor 1.0
[29,neuromodulated_stdp_synapse_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[30,neuromodulated_stdp_synapse_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[31,neuromodulated_stdp_synapse_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[32,GLOBAL, INFO]: State variables that will be moved from synapse to neuron: ['post_tr']
[33,GLOBAL, INFO]: Parameters that will be copied from synapse to neuron: ['tau_tr_post']
[34,GLOBAL, INFO]: Moving state var defining equation(s) post_tr
[35,GLOBAL, INFO]: Moving state variables for equation(s) post_tr
[36,GLOBAL, INFO]: Moving definition of post_tr from synapse to neuron
[37,GLOBAL, INFO]: Moving statement post_tr += 1.0
[38,GLOBAL, INFO]: In synapse: replacing ``continuous`` type input ports that are connected to postsynaptic neuron with suffixed external variable references
[39,GLOBAL, INFO]: Copying parameters from synapse to neuron...
[40,GLOBAL, INFO]: Copying definition of tau_tr_post from synapse to neuron
[41,GLOBAL, INFO]: Adding suffix to variables in spike updates
[42,GLOBAL, INFO]: In synapse: replacing variables with suffixed external variable references
[43,GLOBAL, INFO]: • Replacing variable post_tr
[44,GLOBAL, INFO]: ASTSimpleExpression replacement made (var = post_tr__for_neuromodulated_stdp_synapse_nestml) in expression: A_minus * post_tr
[47,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[48,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[49,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
INFO:Analysing input:
INFO:{
"dynamics": [
{
"expression": "I_syn_exc' = (-I_syn_exc) / tau_syn_exc",
"initial_values": {
"I_syn_exc": "0"
}
},
{
"expression": "I_syn_inh' = (-I_syn_inh) / tau_syn_inh",
"initial_values": {
"I_syn_inh": "0"
}
},
{
"expression": "V_m' = (-(V_m - E_L)) / tau_m + (I_syn_exc - I_syn_inh + I_e + I_stim) / C_m",
"initial_values": {
"V_m": "E_L"
}
}
],
"options": {
"output_timestep_symbol": "__h"
},
"parameters": {
"C_m": "250",
"E_L": "(-70)",
"I_e": "0",
"V_reset": "(-70)",
"V_th": "(-55)",
"refr_T": "2",
"tau_m": "10",
"tau_syn_exc": "2",
"tau_syn_inh": "2"
}
}
INFO:Processing global options...
INFO:Processing input shapes...
INFO:
Processing differential-equation form shape I_syn_exc with defining expression = "(-I_syn_exc) / tau_syn_exc"
INFO: Returning shape: Shape "I_syn_exc" of order 1
INFO:Shape I_syn_exc: reconstituting expression -I_syn_exc/tau_syn_exc
INFO:
Processing differential-equation form shape I_syn_inh with defining expression = "(-I_syn_inh) / tau_syn_inh"
INFO: Returning shape: Shape "I_syn_inh" of order 1
INFO:Shape I_syn_inh: reconstituting expression -I_syn_inh/tau_syn_inh
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + (I_syn_exc - I_syn_inh + I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m + I_syn_exc/C_m - I_syn_inh/C_m
INFO:All known variables: [I_syn_exc, I_syn_inh, V_m], all parameters used in ODEs: {tau_syn_exc, E_L, tau_m, I_e, C_m, I_stim, tau_syn_inh}
INFO:No numerical value specified for parameter "I_stim"
INFO:
Processing differential-equation form shape I_syn_exc with defining expression = "(-I_syn_exc) / tau_syn_exc"
INFO: Returning shape: Shape "I_syn_exc" of order 1
INFO:
Processing differential-equation form shape I_syn_inh with defining expression = "(-I_syn_inh) / tau_syn_inh"
INFO: Returning shape: Shape "I_syn_inh" of order 1
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + (I_syn_exc - I_syn_inh + I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:Shape I_syn_exc: reconstituting expression -I_syn_exc/tau_syn_exc
INFO:Shape I_syn_inh: reconstituting expression -I_syn_inh/tau_syn_inh
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m + I_syn_exc/C_m - I_syn_inh/C_m
INFO:Finding analytically solvable equations...
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph.dot
[50,GLOBAL, INFO]: Successfully constructed neuron-synapse pair iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml, neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml
[51,GLOBAL, INFO]: Analysing/transforming model 'iaf_psc_exp_neuron_nestml'
[52,iaf_psc_exp_neuron_nestml, INFO, [55:0;115:0]]: Starts processing of the model 'iaf_psc_exp_neuron_nestml'
INFO:Shape I_syn_exc: reconstituting expression -I_syn_exc/tau_syn_exc
INFO:Shape I_syn_inh: reconstituting expression -I_syn_inh/tau_syn_inh
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m + I_syn_exc/C_m - I_syn_inh/C_m
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable_before_propagated.dot
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable.dot
INFO:Generating propagators for the following symbols: I_syn_exc, I_syn_inh, V_m
WARNING:Under certain conditions, the propagator matrix is singular (contains infinities).
WARNING:List of all conditions that result in a singular propagator:
WARNING: tau_m = tau_syn_exc
WARNING: tau_m = tau_syn_inh
INFO:update_expr[I_syn_exc] = I_syn_exc*__P__I_syn_exc__I_syn_exc
INFO:update_expr[I_syn_inh] = I_syn_inh*__P__I_syn_inh__I_syn_inh
INFO:update_expr[V_m] = -E_L*__P__V_m__V_m + E_L + I_syn_exc*__P__V_m__I_syn_exc + I_syn_inh*__P__V_m__I_syn_inh + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m
WARNING:Not preserving expression for variable "I_syn_exc" as it is solved by propagator solver
WARNING:Not preserving expression for variable "I_syn_inh" as it is solved by propagator solver
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
INFO:In ode-toolbox: returning outdict =
INFO:[
{
"initial_values": {
"I_syn_exc": "0",
"I_syn_inh": "0",
"V_m": "E_L"
},
"parameters": {
"C_m": "250.000000000000",
"E_L": "-70.0000000000000",
"I_e": "0",
"tau_m": "10.0000000000000",
"tau_syn_exc": "2.00000000000000",
"tau_syn_inh": "2.00000000000000"
},
"propagators": {
"__P__I_syn_exc__I_syn_exc": "exp(-__h/tau_syn_exc)",
"__P__I_syn_inh__I_syn_inh": "exp(-__h/tau_syn_inh)",
"__P__V_m__I_syn_exc": "tau_m*tau_syn_exc*(-exp(__h/tau_m) + exp(__h/tau_syn_exc))*exp(-__h*(tau_m + tau_syn_exc)/(tau_m*tau_syn_exc))/(C_m*(tau_m - tau_syn_exc))",
"__P__V_m__I_syn_inh": "tau_m*tau_syn_inh*(exp(__h/tau_m) - exp(__h/tau_syn_inh))*exp(-__h/tau_syn_inh - __h/tau_m)/(C_m*(tau_m - tau_syn_inh))",
"__P__V_m__V_m": "exp(-__h/tau_m)"
},
"solver": "analytical",
"state_variables": [
"I_syn_exc",
"I_syn_inh",
"V_m"
],
"update_expressions": {
"I_syn_exc": "I_syn_exc*__P__I_syn_exc__I_syn_exc",
"I_syn_inh": "I_syn_inh*__P__I_syn_inh__I_syn_inh",
"V_m": "-E_L*__P__V_m__V_m + E_L + I_syn_exc*__P__V_m__I_syn_exc + I_syn_inh*__P__V_m__I_syn_inh + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m"
}
}
]
INFO:Analysing input:
INFO:{
"dynamics": [
{
"expression": "I_syn_exc' = (-I_syn_exc) / tau_syn_exc",
"initial_values": {
"I_syn_exc": "0"
}
},
{
"expression": "I_syn_inh' = (-I_syn_inh) / tau_syn_inh",
"initial_values": {
"I_syn_inh": "0"
}
},
{
"expression": "V_m' = (-(V_m - E_L)) / tau_m + (I_syn_exc - I_syn_inh + I_e + I_stim) / C_m",
"initial_values": {
"V_m": "E_L"
}
},
{
"expression": "post_tr__for_neuromodulated_stdp_synapse_nestml' = (-post_tr__for_neuromodulated_stdp_synapse_nestml) / tau_tr_post__for_neuromodulated_stdp_synapse_nestml",
"initial_values": {
"post_tr__for_neuromodulated_stdp_synapse_nestml": "0.0"
}
}
],
"options": {
"output_timestep_symbol": "__h"
},
"parameters": {
"C_m": "250",
"E_L": "(-70)",
"I_e": "0",
"V_reset": "(-70)",
"V_th": "(-55)",
"refr_T": "2",
"tau_m": "10",
"tau_syn_exc": "2",
"tau_syn_inh": "2",
"tau_tr_post__for_neuromodulated_stdp_synapse_nestml": "20"
}
}
INFO:Processing global options...
INFO:Processing input shapes...
INFO:
Processing differential-equation form shape I_syn_exc with defining expression = "(-I_syn_exc) / tau_syn_exc"
INFO: Returning shape: Shape "I_syn_exc" of order 1
INFO:Shape I_syn_exc: reconstituting expression -I_syn_exc/tau_syn_exc
INFO:
Processing differential-equation form shape I_syn_inh with defining expression = "(-I_syn_inh) / tau_syn_inh"
INFO: Returning shape: Shape "I_syn_inh" of order 1
INFO:Shape I_syn_inh: reconstituting expression -I_syn_inh/tau_syn_inh
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + (I_syn_exc - I_syn_inh + I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m + I_syn_exc/C_m - I_syn_inh/C_m
INFO:
Processing differential-equation form shape post_tr__for_neuromodulated_stdp_synapse_nestml with defining expression = "(-post_tr__for_neuromodulated_stdp_synapse_nestml) / tau_tr_post__for_neuromodulated_stdp_synapse_nestml"
INFO: Returning shape: Shape "post_tr__for_neuromodulated_stdp_synapse_nestml" of order 1
INFO:Shape post_tr__for_neuromodulated_stdp_synapse_nestml: reconstituting expression -post_tr__for_neuromodulated_stdp_synapse_nestml/tau_tr_post__for_neuromodulated_stdp_synapse_nestml
INFO:All known variables: [I_syn_exc, I_syn_inh, V_m, post_tr__for_neuromodulated_stdp_synapse_nestml], all parameters used in ODEs: {tau_syn_exc, tau_tr_post__for_neuromodulated_stdp_synapse_nestml, E_L, tau_m, I_e, C_m, I_stim, tau_syn_inh}
INFO:No numerical value specified for parameter "I_stim"
INFO:
Processing differential-equation form shape I_syn_exc with defining expression = "(-I_syn_exc) / tau_syn_exc"
INFO: Returning shape: Shape "I_syn_exc" of order 1
INFO:
Processing differential-equation form shape I_syn_inh with defining expression = "(-I_syn_inh) / tau_syn_inh"
INFO: Returning shape: Shape "I_syn_inh" of order 1
INFO:
Processing differential-equation form shape V_m with defining expression = "(-(V_m - E_L)) / tau_m + (I_syn_exc - I_syn_inh + I_e + I_stim) / C_m"
INFO: Returning shape: Shape "V_m" of order 1
INFO:
Processing differential-equation form shape post_tr__for_neuromodulated_stdp_synapse_nestml with defining expression = "(-post_tr__for_neuromodulated_stdp_synapse_nestml) / tau_tr_post__for_neuromodulated_stdp_synapse_nestml"
INFO: Returning shape: Shape "post_tr__for_neuromodulated_stdp_synapse_nestml" of order 1
INFO:Shape I_syn_exc: reconstituting expression -I_syn_exc/tau_syn_exc
INFO:Shape I_syn_inh: reconstituting expression -I_syn_inh/tau_syn_inh
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m + I_syn_exc/C_m - I_syn_inh/C_m
INFO:Shape post_tr__for_neuromodulated_stdp_synapse_nestml: reconstituting expression -post_tr__for_neuromodulated_stdp_synapse_nestml/tau_tr_post__for_neuromodulated_stdp_synapse_nestml
INFO:Finding analytically solvable equations...
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph.dot
[54,GLOBAL, INFO]: Analysing/transforming model 'iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml'
[55,iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml, INFO, [55:0;115:0]]: Starts processing of the model 'iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml'
INFO:Shape I_syn_exc: reconstituting expression -I_syn_exc/tau_syn_exc
INFO:Shape I_syn_inh: reconstituting expression -I_syn_inh/tau_syn_inh
INFO:Shape V_m: reconstituting expression E_L/tau_m - V_m/tau_m + I_e/C_m + I_stim/C_m + I_syn_exc/C_m - I_syn_inh/C_m
INFO:Shape post_tr__for_neuromodulated_stdp_synapse_nestml: reconstituting expression -post_tr__for_neuromodulated_stdp_synapse_nestml/tau_tr_post__for_neuromodulated_stdp_synapse_nestml
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable_before_propagated.dot
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable.dot
INFO:Generating propagators for the following symbols: I_syn_exc, I_syn_inh, V_m, post_tr__for_neuromodulated_stdp_synapse_nestml
WARNING:Under certain conditions, the propagator matrix is singular (contains infinities).
WARNING:List of all conditions that result in a singular propagator:
WARNING: tau_m = tau_syn_exc
WARNING: tau_m = tau_syn_inh
INFO:update_expr[I_syn_exc] = I_syn_exc*__P__I_syn_exc__I_syn_exc
INFO:update_expr[I_syn_inh] = I_syn_inh*__P__I_syn_inh__I_syn_inh
INFO:update_expr[V_m] = -E_L*__P__V_m__V_m + E_L + I_syn_exc*__P__V_m__I_syn_exc + I_syn_inh*__P__V_m__I_syn_inh + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m
INFO:update_expr[post_tr__for_neuromodulated_stdp_synapse_nestml] = __P__post_tr__for_neuromodulated_stdp_synapse_nestml__post_tr__for_neuromodulated_stdp_synapse_nestml*post_tr__for_neuromodulated_stdp_synapse_nestml
WARNING:Not preserving expression for variable "I_syn_exc" as it is solved by propagator solver
WARNING:Not preserving expression for variable "I_syn_inh" as it is solved by propagator solver
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
WARNING:Not preserving expression for variable "post_tr__for_neuromodulated_stdp_synapse_nestml" as it is solved by propagator solver
INFO:In ode-toolbox: returning outdict =
INFO:[
{
"initial_values": {
"I_syn_exc": "0",
"I_syn_inh": "0",
"V_m": "E_L",
"post_tr__for_neuromodulated_stdp_synapse_nestml": "0.0"
},
"parameters": {
"C_m": "250.000000000000",
"E_L": "-70.0000000000000",
"I_e": "0",
"tau_m": "10.0000000000000",
"tau_syn_exc": "2.00000000000000",
"tau_syn_inh": "2.00000000000000",
"tau_tr_post__for_neuromodulated_stdp_synapse_nestml": "20.0000000000000"
},
"propagators": {
"__P__I_syn_exc__I_syn_exc": "exp(-__h/tau_syn_exc)",
"__P__I_syn_inh__I_syn_inh": "exp(-__h/tau_syn_inh)",
"__P__V_m__I_syn_exc": "tau_m*tau_syn_exc*(-exp(__h/tau_m) + exp(__h/tau_syn_exc))*exp(-__h*(tau_m + tau_syn_exc)/(tau_m*tau_syn_exc))/(C_m*(tau_m - tau_syn_exc))",
"__P__V_m__I_syn_inh": "tau_m*tau_syn_inh*(exp(__h/tau_m) - exp(__h/tau_syn_inh))*exp(-__h/tau_syn_inh - __h/tau_m)/(C_m*(tau_m - tau_syn_inh))",
"__P__V_m__V_m": "exp(-__h/tau_m)",
"__P__post_tr__for_neuromodulated_stdp_synapse_nestml__post_tr__for_neuromodulated_stdp_synapse_nestml": "exp(-__h/tau_tr_post__for_neuromodulated_stdp_synapse_nestml)"
},
"solver": "analytical",
"state_variables": [
"I_syn_exc",
"I_syn_inh",
"V_m",
"post_tr__for_neuromodulated_stdp_synapse_nestml"
],
"update_expressions": {
"I_syn_exc": "I_syn_exc*__P__I_syn_exc__I_syn_exc",
"I_syn_inh": "I_syn_inh*__P__I_syn_inh__I_syn_inh",
"V_m": "-E_L*__P__V_m__V_m + E_L + I_syn_exc*__P__V_m__I_syn_exc + I_syn_inh*__P__V_m__I_syn_inh + V_m*__P__V_m__V_m - I_e*__P__V_m__V_m*tau_m/C_m + I_e*tau_m/C_m - I_stim*__P__V_m__V_m*tau_m/C_m + I_stim*tau_m/C_m",
"post_tr__for_neuromodulated_stdp_synapse_nestml": "__P__post_tr__for_neuromodulated_stdp_synapse_nestml__post_tr__for_neuromodulated_stdp_synapse_nestml*post_tr__for_neuromodulated_stdp_synapse_nestml"
}
}
]
INFO:Analysing input:
INFO:{
"dynamics": [
{
"expression": "pre_tr' = (-pre_tr) / tau_tr_pre",
"initial_values": {
"pre_tr": "0.0"
}
}
],
"options": {
"output_timestep_symbol": "__h"
},
"parameters": {
"A_minus": "1.5",
"A_plus": "1.0",
"A_vt": "1.0",
"Wmax": "200.0",
"Wmin": "0.0",
"b": "0.0",
"d": "1",
"tau_c": "1000",
"tau_n": "200",
"tau_tr_post": "20",
"tau_tr_pre": "20"
}
}
INFO:Processing global options...
INFO:Processing input shapes...
INFO:
Processing differential-equation form shape pre_tr with defining expression = "(-pre_tr) / tau_tr_pre"
INFO: Returning shape: Shape "pre_tr" of order 1
INFO:Shape pre_tr: reconstituting expression -pre_tr/tau_tr_pre
INFO:All known variables: [pre_tr], all parameters used in ODEs: {tau_tr_pre}
INFO:
Processing differential-equation form shape pre_tr with defining expression = "(-pre_tr) / tau_tr_pre"
INFO: Returning shape: Shape "pre_tr" of order 1
INFO:Shape pre_tr: reconstituting expression -pre_tr/tau_tr_pre
INFO:Finding analytically solvable equations...
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph.dot
INFO:Shape pre_tr: reconstituting expression -pre_tr/tau_tr_pre
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable_before_propagated.dot
[57,GLOBAL, INFO]: Analysing/transforming synapse neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.
[58,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [2:0;66:0]]: Starts processing of the model 'neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml'
INFO:Saving dependency graph plot to /tmp/ode_dependency_graph_analytically_solvable.dot
INFO:Generating propagators for the following symbols: pre_tr
INFO:update_expr[pre_tr] = __P__pre_tr__pre_tr*pre_tr
WARNING:Not preserving expression for variable "pre_tr" as it is solved by propagator solver
INFO:In ode-toolbox: returning outdict =
INFO:[
{
"initial_values": {
"pre_tr": "0.0"
},
"parameters": {
"tau_tr_pre": "20.0000000000000"
},
"propagators": {
"__P__pre_tr__pre_tr": "exp(-__h/tau_tr_pre)"
},
"solver": "analytical",
"state_variables": [
"pre_tr"
],
"update_expressions": {
"pre_tr": "__P__pre_tr__pre_tr*pre_tr"
}
}
]
[60,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[61,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[62,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[64,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, WARNING, [12:8;12:28]]: Variable 'd' has the same name as a physical unit!
[65,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [40:13;40:20]]: Implicit casting from (compatible) type '1 / ms' to 'real'.
[66,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [63:13;63:123]]: Implicit casting from (compatible) type 'ms' to 'real'.
[67,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.cpp
[68,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.h
[69,iaf_psc_exp_neuron_nestml, INFO, [55:0;115:0]]: Successfully generated code for the model: 'iaf_psc_exp_neuron_nestml' in: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
[70,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp
[71,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.h
[72,iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml, INFO, [55:0;115:0]]: Successfully generated code for the model: 'iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml' in: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
Generating code for the synapse neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.
[73,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h
[74,neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml, INFO, [2:0;66:0]]: Successfully generated code for the model: 'neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml' in: '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
[75,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.cpp
[76,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.h
[77,GLOBAL, INFO]: Rendering template /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/CMakeLists.txt
[78,GLOBAL, INFO]: Successfully generated NEST module code in '/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target' !
CMake Warning (dev) at CMakeLists.txt:95 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module' using
make
make install
The library file libnestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.so will be installed to
/tmp/nestml_target_nxqmze5r
The module can be loaded into NEST using
(nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module) Install (in SLI)
nest.Install(nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target
[ 25%] Building CXX object CMakeFiles/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module_module.dir/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.o
[ 50%] Building CXX object CMakeFiles/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module_module.dir/iaf_psc_exp_neuron_nestml.o
[ 75%] Building CXX object CMakeFiles/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module_module.dir/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp: In member function ‘void iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp:196:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
196 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp: In member function ‘virtual void iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp:310:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
310 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml.cpp:305:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
305 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.cpp: In member function ‘void iaf_psc_exp_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.cpp:186:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
186 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_exp_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.cpp:289:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
289 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/iaf_psc_exp_neuron_nestml.cpp:284:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
284 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
In file included from /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.cpp:36:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierPtrRport>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:62:5: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:671:104: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:862:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
862 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::recompute_internal_variables() [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:876:3: required from ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierPtrRport]’
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierPtrRport>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:62:5: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:671:104: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:849:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
849 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:103:34: required from ‘void nest::ModelManager::register_specific_connection_model_(const std::string&) [with CompleteConnecionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:67:80: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:671:104: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:862:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
862 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::recompute_internal_variables() [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:876:3: required from ‘nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml() [with targetidentifierT = nest::TargetIdentifierIndex]’
/home/charl/julich/nest-simulator-install/include/nest/connector_model.h:164:25: required from ‘nest::GenericConnectorModel<ConnectionT>::GenericConnectorModel(std::string) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:103:34: required from ‘void nest::ModelManager::register_specific_connection_model_(const std::string&) [with CompleteConnecionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/model_manager_impl.h:67:80: required from ‘void nest::ModelManager::register_connection_model(const std::string&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nest-simulator-install/include/nest/nest_impl.h:37:70: required from ‘void nest::register_connection_model(const std::string&) [with ConnectorModelT = neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml; std::string = std::__cxx11::basic_string<char>]’
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:671:104: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:849:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
849 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:589:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
589 | auto get_t = [_tr_t](){ return _tr_t; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:614:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
614 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:649:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
649 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:517:18: warning: unused variable ‘__resolution’ [-Wunused-variable]
517 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:519:10: warning: variable ‘get_thread’ set but not used [-Wunused-but-set-variable]
519 | auto get_thread = [tid]()
| ^~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::trigger_update_weight(size_t, const std::vector<nest::spikecounter>&, double, const CommonPropertiesType&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int; CommonPropertiesType = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:446:38: required from ‘void nest::Connector<ConnectionT>::trigger_update_weight(long int, size_t, const std::vector<nest::spikecounter>&, double, const std::vector<nest::ConnectorModel*>&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:433:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:1009:18: warning: unused variable ‘_tr_t’ [-Wunused-variable]
1009 | const double _tr_t = start->t_;
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:991:10: warning: unused variable ‘timestep’ [-Wunused-variable]
991 | double timestep = 0;
| ^~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:589:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
589 | auto get_t = [_tr_t](){ return _tr_t; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:614:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
614 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:649:14: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
649 | auto get_t = [__t_spike](){ return __t_spike; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:517:18: warning: unused variable ‘__resolution’ [-Wunused-variable]
517 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:519:10: warning: variable ‘get_thread’ set but not used [-Wunused-but-set-variable]
519 | auto get_thread = [tid]()
| ^~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::trigger_update_weight(size_t, const std::vector<nest::spikecounter>&, double, const CommonPropertiesType&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int; CommonPropertiesType = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties]’:
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:446:38: required from ‘void nest::Connector<ConnectionT>::trigger_update_weight(long int, size_t, const std::vector<nest::spikecounter>&, double, const std::vector<nest::ConnectorModel*>&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:433:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:1009:18: warning: unused variable ‘_tr_t’ [-Wunused-variable]
1009 | const double _tr_t = start->t_;
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:991:10: warning: unused variable ‘timestep’ [-Wunused-variable]
991 | double timestep = 0;
| ^~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::process_mod_spikes_spikes_(const std::vector<nest::spikecounter>&, double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:563:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:699:12: warning: unused variable ‘cd’ [-Wunused-variable]
699 | double cd;
| ^~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::update_internal_state_(double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:584:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierPtrRport; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierPtrRport>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:935:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
935 | auto get_t = [t_start](){ return t_start; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::process_mod_spikes_spikes_(const std::vector<nest::spikecounter>&, double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:563:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:699:12: warning: unused variable ‘cd’ [-Wunused-variable]
699 | double cd;
| ^~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h: In instantiation of ‘void nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::update_internal_state_(double, double, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex]’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:584:9: required from ‘bool nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<targetidentifierT>::send(nest::Event&, size_t, const nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestmlCommonSynapseProperties&) [with targetidentifierT = nest::TargetIdentifierIndex; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:391:22: required from ‘void nest::Connector<ConnectionT>::send_to_all(size_t, const std::vector<nest::ConnectorModel*>&, nest::Event&) [with ConnectionT = nest::neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml<nest::TargetIdentifierIndex>; size_t = long unsigned int]’
/home/charl/julich/nest-simulator-install/include/nest/connector_base.h:383:3: required from here
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/stdp_dopa_synapse/target/neuromodulated_stdp_synapse_nestml__with_iaf_psc_exp_neuron_nestml.h:935:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
935 | auto get_t = [t_start](){ return t_start; }; // do not remove, this is in case the predefined time variable ``t`` is used in the NESTML model
| ^~~~~
[100%] Linking CXX shared module nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.so
[100%] Built target nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module_module
[100%] Built target nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_nxqmze5r/nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module.so
Now, we define the network and the simulation parameters.
[16]:
# simulation parameters
dt = .1 # the resolution in ms
delay = 1. # synaptic delay in ms
total_t_sim = 10000. # [ms]
# parameters for balanced network
g = 4. # ratio inhibitory weight/excitatory weight
epsilon = .1 # connection probability
NE = 800 # number of excitatory neurons
NI = 200 # number of inhibitory neurons
N_neurons = NE + NI # number of neurons in total
N_rec = 50 # record from 50 neurons
CE = int(epsilon * NE) # number of excitatory synapses per neuron
CI = int(epsilon * NI) # number of inhibitory synapses per neuron
C_tot = int(CI + CE) # total number of synapses per neuron
# neuron parameters
tauSyn = 1. # synaptic time constant [ms]
tauMem = 10. # time constant of membrane potential [ms]
CMem = 300. # capacitance of membrane [pF]
neuron_params_exc = {"C_m": CMem,
"tau_m": tauMem,
"tau_syn_exc": tauSyn,
"tau_syn_inh": tauSyn,
"refr_T": 4.0,
"E_L": -65.,
"V_reset": -70.,
"V_m": -65.,
"V_th": -55.4,
"I_e": 0. # [pA]
}
neuron_params_inh = {"C_m": CMem,
"tau_m": tauMem,
"tau_syn_exc": tauSyn,
"tau_syn_inh": tauSyn,
"refr_T": 2.0,
"E_L": -65.,
"V_reset": -70.,
"V_m": -65.,
"V_th": -56.4}
# J_ex should be large enough so that when stimulus excites the subgroup cells,
# the subgroup cells cause an excitatory transient in the network to establish
# a causal STDP timing and positive eligibility trace in the synapses
J_ex = 300. # amplitude of excitatory postsynaptic current
J_in = -g * J_ex # amplitude of inhibitory postsynaptic current
J_poisson = 2500.
J_stim = 5000.
p_rate = 5. # external Poisson generator rate [s^-1]
# synapse parameters
learning_rate = .1 # multiplier for weight updates
tau_c = 200. # [ms]
tau_n = 200. # [ms]
# stimulus parameters
n_subgroups = 2 # = n_stimuli
subgroup_size = 50 # per subgroup, this many neurons are stimulated when stimulus is presented
reinforced_subgroup_idx = 0
stimulus_rate = 5. # [s^-1]
min_stimulus_presentation_delay = 10. # minimum time between presenting stimuli [ms]
min_dopa_reinforcement_delay = 10. # [ms]
max_dopa_reinforcement_delay = 30. # [ms]
With the parameters defined, we are ready to instantiate and connect the network.
[17]:
nest.ResetKernel()
nest.Install(module_name) # load dynamic library (NEST extension module) into NEST kernel
nest.set_verbosity("M_ALL")
nest.local_num_threads = 4
nest.resolution = dt
nest.print_time = True
nest.overwrite_files = True
nodes_ex = nest.Create(neuron_model_name, NE, params=neuron_params_exc)
nodes_in = nest.Create(neuron_model_name, NI, params=neuron_params_inh)
noise = nest.Create("poisson_generator", params={"rate": p_rate})
vt_spike_times = []
vt_sg = nest.Create("spike_generator",
params={"spike_times": vt_spike_times,
"allow_offgrid_times": True})
espikes = nest.Create("spike_recorder")
ispikes = nest.Create("spike_recorder")
spikedet_vt = nest.Create("spike_recorder")
# create volume transmitter
vt = nest.Create("volume_transmitter")
vt_parrot = nest.Create("parrot_neuron")
nest.Connect(vt_sg, vt_parrot)
nest.Connect(vt_parrot, vt, syn_spec={"synapse_model": "static_synapse",
"weight": 1.,
"delay": 1.}) # delay is ignored
# set up custom synapse models
wr = nest.Create("weight_recorder")
nest.CopyModel(synapse_model_name, "excitatory",
{"weight_recorder": wr, "w": J_ex, "d": delay, "receptor_type": 0,
"volume_transmitter": vt, "A_plus": learning_rate * 1., "A_minus": learning_rate * 1.5,
"tau_n": tau_n,
"tau_c": tau_c})
nest.CopyModel("static_synapse", "inhibitory",
{"weight": J_in, "delay": delay})
nest.CopyModel("static_synapse", "poisson",
{"weight": J_poisson, "delay": delay})
# make subgroups: pick from excitatory population. subgroups can overlap, but
# each group consists of `subgroup_size` unique neurons
subgroup_indices = n_subgroups * [[]]
for i in range(n_subgroups):
ids_nonoverlapping = False
# TODO: replace while loop with:
# subgroup_indices[i] = np.sort(np.random.choice(NE, size=subgroup_size, replace=False))
while not ids_nonoverlapping:
ids = np.random.randint(0, NE, subgroup_size)
ids_nonoverlapping = len(np.unique(ids)) == subgroup_size
ids.sort()
subgroup_indices[i] = ids
# make one spike generator and one parrot neuron for each subgroup
stim_sg = nest.Create("spike_generator", n_subgroups)
stim_parrots = nest.Create("parrot_neuron", n_subgroups)
# make recording devices
stim_spikes_rec = nest.Create("spike_recorder")
mm = nest.Create("multimeter", params={'record_from': ['V_m'], 'interval': dt})
mms = [nest.Create("multimeter", params={'record_from': ['V_m'], 'interval': dt}) for _ in range(10)]
# connect everything up
nest.Connect(stim_parrots, stim_spikes_rec, syn_spec="static_synapse")
nest.Connect(noise, nodes_ex + nodes_in, syn_spec="poisson")
nest.Connect(mm, nodes_ex[0])
[nest.Connect(mms[i], nodes_ex[i]) for i in range(10)]
nest.Connect(stim_sg, stim_parrots, "one_to_one")
for i in range(n_subgroups):
nest.Connect(stim_parrots[i], nodes_ex[subgroup_indices[i]], "all_to_all", syn_spec={"weight": J_stim})
conn_params_ex = {'rule': 'fixed_indegree', 'indegree': CE}
nest.Connect(nodes_ex, nodes_ex + nodes_in, conn_params_ex, "excitatory")
conn_params_in = {'rule': 'fixed_indegree', 'indegree': CI}
nest.Connect(nodes_in, nodes_ex + nodes_in, conn_params_in, "inhibitory")
nest.Connect(vt_parrot, spikedet_vt)
nest.Connect(nodes_ex, espikes, syn_spec="static_synapse")
nest.Connect(nodes_in, ispikes, syn_spec="static_synapse")
# generate stimulus timings (input stimulus and reinforcement signal)
t_dopa_spikes = []
t_pre_sg_spikes = [[] for _ in range(n_subgroups)] # mapping from subgroup_idx to a list of spike (or presentation) times of that subgroup
t = 0. # [ms]
ev_timestamps = []
while t < total_t_sim:
# jump to time of next stimulus presentation
dt_next_stimulus = max(min_stimulus_presentation_delay, np.round(random.expovariate(stimulus_rate) * 1000)) # [ms]
t += dt_next_stimulus
ev_timestamps.append(t)
# apply stimulus
subgroup_idx = np.random.randint(0, n_subgroups)
t_pre_sg_spikes[subgroup_idx].append(t)
# reinforce?
if subgroup_idx == reinforced_subgroup_idx:
# fire a dopa spike some time after the current time
t_dopa_spike = t + min_dopa_reinforcement_delay + np.random.randint(max_dopa_reinforcement_delay - min_dopa_reinforcement_delay)
t_dopa_spikes.append(t_dopa_spike)
print("--> Stimuli will be presented at times: " + str(ev_timestamps))
# set the spike times in the spike generators
for i in range(n_subgroups):
t_pre_sg_spikes[i].sort()
stim_sg[i].spike_times = t_pre_sg_spikes[i]
t_dopa_spikes.sort()
vt_sg.spike_times = t_dopa_spikes
print("--> t_dopa_spikes = " + str(t_dopa_spikes))
Apr 19 11:34:22 Install [Info]:
loaded module nestml_6a0e5b32a83c4b3a83ce6c87a2445436_module
Apr 19 11:34:22 iaf_psc_exp_neuron_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:34:22 iaf_psc_exp_neuron_nestml__with_neuromodulated_stdp_synapse_nestml [Warning]:
Simulation resolution has changed. Internal state and parameters of the
model have been reset!
Apr 19 11:34:22 SimulationManager::set_status [Info]:
Temporal resolution changed from 0.1 to 0.1 ms.
--> Stimuli will be presented at times: [137.0, 168.0, 197.0, 242.0, 351.0, 400.0, 410.0, 712.0, 1254.0, 1284.0, 1651.0, 1858.0, 1921.0, 2093.0, 2210.0, 2242.0, 2252.0, 2675.0, 2734.0, 2768.0, 3022.0, 3040.0, 3229.0, 3371.0, 3434.0, 3712.0, 3887.0, 4080.0, 4209.0, 4808.0, 5490.0, 5581.0, 5621.0, 5701.0, 6040.0, 6262.0, 6491.0, 6754.0, 6837.0, 6980.0, 7042.0, 7222.0, 7273.0, 7472.0, 8103.0, 8126.0, 8451.0, 8489.0, 8676.0, 8745.0, 8876.0, 9068.0, 9152.0, 9224.0, 9433.0, 9447.0, 9580.0, 9633.0, 9643.0, 9920.0, 10113.0]
--> t_dopa_spikes = [163.0, 209.0, 425.0, 731.0, 1883.0, 2106.0, 2230.0, 2701.0, 2785.0, 3050.0, 3052.0, 3395.0, 3904.0, 5514.0, 5633.0, 5721.0, 6055.0, 6290.0, 6510.0, 6781.0, 6999.0, 7069.0, 7500.0, 8126.0, 8463.0, 8768.0, 9164.0, 9237.0, 9449.0, 9459.0, 9593.0]
Run the simulation. Instead of just running from start to finish in one go:
[18]:
# nest.Simulate(total_t_sim)
we split the simulation into equally-sized chunks, so that we can measure and record the state of some internal variables inbetween:
[19]:
def run_chunked_simulation(n_chunks, all_nodes, reinforced_group_nodes, not_reinforced_group_nodes):
# init log
log = {}
log["t"] = []
log["w_net"] = []
recordables = ["c_sum", "w_avg", "n_avg"]
for group in ["reinforced_group", "not_reinforced_group"]:
log[group] = {}
for recordable in recordables:
log[group][recordable] = []
nest.Prepare()
for i in range(n_chunks):
print(str(np.round(100 * i / n_chunks)) + "%")
# simulate one chunk
nest.Run(total_t_sim // n_chunks)
# log current values
log["t"].append(nest.GetKernelStatus("biological_time"))
syn_reinforced_subgroup = nest.GetConnections(source=reinforced_group_nodes, synapse_model="excitatory")
syn_nonreinforced_subgroup = nest.GetConnections(source=not_reinforced_group_nodes, synapse_model="excitatory")
syn_all = nest.GetConnections(source=all_nodes, synapse_model="excitatory")
log["w_net"].append(np.mean(syn_all.w))
log["reinforced_group"]["w_avg"].append(np.mean(syn_reinforced_subgroup.get("w")))
log["not_reinforced_group"]["w_avg"].append(np.mean(syn_nonreinforced_subgroup.get("w")))
log["reinforced_group"]["c_sum"].append(np.sum(syn_reinforced_subgroup.get("c")))
log["not_reinforced_group"]["c_sum"].append(np.sum(syn_nonreinforced_subgroup.get("c")))
log["reinforced_group"]["n_avg"].append(np.mean(syn_reinforced_subgroup.get("n")))
log["not_reinforced_group"]["n_avg"].append(np.mean(syn_nonreinforced_subgroup.get("n")))
nest.Cleanup()
return log
[20]:
all_nodes = nodes_ex
reinforced_group_nodes = nodes_ex[subgroup_indices[reinforced_subgroup_idx]]
not_reinforced_group_nodes = nodes_ex[subgroup_indices[1 - reinforced_subgroup_idx]]
n_chunks = 100
log = run_chunked_simulation(n_chunks,
all_nodes,
reinforced_group_nodes,
not_reinforced_group_nodes)
0.0%
Apr 19 11:34:22 NodeManager::prepare_nodes [Info]:
Preparing 1087 nodes for simulation.
Apr 19 11:34:22 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 100.0 ms, Real-time factor: 3.9082
Apr 19 11:34:23 SimulationManager::run [Info]:
Simulation finished.
1.0%
Apr 19 11:34:25 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 200.0 ms, Real-time factor: 8.043620
Apr 19 11:34:26 SimulationManager::run [Info]:
Simulation finished.
2.0%
Apr 19 11:34:29 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 300.0 ms, Real-time factor: 12.32186
Apr 19 11:34:29 SimulationManager::run [Info]:
Simulation finished.
3.0%
Apr 19 11:34:31 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 400.0 ms, Real-time factor: 17.752280
Apr 19 11:34:32 SimulationManager::run [Info]:
Simulation finished.
4.0%
Apr 19 11:34:35 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 500.0 ms, Real-time factor: 22.306230
Apr 19 11:34:35 SimulationManager::run [Info]:
Simulation finished.
5.0%
Apr 19 11:34:37 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 600.0 ms, Real-time factor: 26.830080
Apr 19 11:34:38 SimulationManager::run [Info]:
Simulation finished.
6.0%
Apr 19 11:34:40 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 700.0 ms, Real-time factor: 31.369480
Apr 19 11:34:41 SimulationManager::run [Info]:
Simulation finished.
7.0%
Apr 19 11:34:43 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 800.0 ms, Real-time factor: 35.899100
Apr 19 11:34:44 SimulationManager::run [Info]:
Simulation finished.
8.0%
Apr 19 11:34:46 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 900.0 ms, Real-time factor: 40.469433
Apr 19 11:34:47 SimulationManager::run [Info]:
Simulation finished.
9.0%
Apr 19 11:34:49 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1000.0 ms, Real-time factor: 44.99197
Apr 19 11:34:50 SimulationManager::run [Info]:
Simulation finished.
10.0%
Apr 19 11:34:52 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1100.0 ms, Real-time factor: 49.572998
Apr 19 11:34:53 SimulationManager::run [Info]:
Simulation finished.
11.0%
Apr 19 11:34:55 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1200.0 ms, Real-time factor: 54.278378
Apr 19 11:34:56 SimulationManager::run [Info]:
Simulation finished.
12.0%
Apr 19 11:34:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1300.0 ms, Real-time factor: 58.832242
Apr 19 11:34:59 SimulationManager::run [Info]:
Simulation finished.
13.0%
Apr 19 11:35:01 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1400.0 ms, Real-time factor: 63.269854
Apr 19 11:35:02 SimulationManager::run [Info]:
Simulation finished.
14.0%
Apr 19 11:35:04 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1500.0 ms, Real-time factor: 67.680667
Apr 19 11:35:05 SimulationManager::run [Info]:
Simulation finished.
15.0%
Apr 19 11:35:07 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1600.0 ms, Real-time factor: 72.092067
Apr 19 11:35:08 SimulationManager::run [Info]:
Simulation finished.
16.0%
Apr 19 11:35:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1700.0 ms, Real-time factor: 76.708270
Apr 19 11:35:11 SimulationManager::run [Info]:
Simulation finished.
17.0%
Apr 19 11:35:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1800.0 ms, Real-time factor: 81.506157
Apr 19 11:35:14 SimulationManager::run [Info]:
Simulation finished.
18.0%
Apr 19 11:35:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 1900.0 ms, Real-time factor: 87.605451
Apr 19 11:35:17 SimulationManager::run [Info]:
Simulation finished.
19.0%
Apr 19 11:35:19 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2000.0 ms, Real-time factor: 93.715430
Apr 19 11:35:20 SimulationManager::run [Info]:
Simulation finished.
20.0%
Apr 19 11:35:23 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2100.0 ms, Real-time factor: 99.787984
Apr 19 11:35:23 SimulationManager::run [Info]:
Simulation finished.
21.0%
Apr 19 11:35:26 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2200.0 ms, Real-time factor: 105.96668
Apr 19 11:35:26 SimulationManager::run [Info]:
Simulation finished.
22.0%
Apr 19 11:35:29 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2300.0 ms, Real-time factor: 110.354440
Apr 19 11:35:29 SimulationManager::run [Info]:
Simulation finished.
23.0%
Apr 19 11:35:32 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2400.0 ms, Real-time factor: 114.504260
Apr 19 11:35:32 SimulationManager::run [Info]:
Simulation finished.
24.0%
Apr 19 11:35:35 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2500.0 ms, Real-time factor: 118.613960
Apr 19 11:35:35 SimulationManager::run [Info]:
Simulation finished.
25.0%
Apr 19 11:35:37 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2600.0 ms, Real-time factor: 122.836110
Apr 19 11:35:38 SimulationManager::run [Info]:
Simulation finished.
26.0%
Apr 19 11:35:40 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2700.0 ms, Real-time factor: 127.048340
Apr 19 11:35:41 SimulationManager::run [Info]:
Simulation finished.
27.0%
Apr 19 11:35:43 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2800.0 ms, Real-time factor: 131.240150
Apr 19 11:35:44 SimulationManager::run [Info]:
Simulation finished.
28.0%
Apr 19 11:35:46 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 2900.0 ms, Real-time factor: 135.360930
Apr 19 11:35:47 SimulationManager::run [Info]:
Simulation finished.
29.0%
Apr 19 11:35:49 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3000.0 ms, Real-time factor: 139.438050
Apr 19 11:35:50 SimulationManager::run [Info]:
Simulation finished.
30.0%
Apr 19 11:35:52 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3100.0 ms, Real-time factor: 143.641890
Apr 19 11:35:53 SimulationManager::run [Info]:
Simulation finished.
31.0%
Apr 19 11:35:55 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3200.0 ms, Real-time factor: 147.738860
Apr 19 11:35:56 SimulationManager::run [Info]:
Simulation finished.
32.0%
Apr 19 11:35:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3300.0 ms, Real-time factor: 151.965970
Apr 19 11:35:59 SimulationManager::run [Info]:
Simulation finished.
33.0%
Apr 19 11:36:01 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3400.0 ms, Real-time factor: 157.258930
Apr 19 11:36:02 SimulationManager::run [Info]:
Simulation finished.
34.0%
Apr 19 11:36:04 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3500.0 ms, Real-time factor: 162.003430
Apr 19 11:36:05 SimulationManager::run [Info]:
Simulation finished.
35.0%
Apr 19 11:36:07 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3600.0 ms, Real-time factor: 166.656710
Apr 19 11:36:08 SimulationManager::run [Info]:
Simulation finished.
36.0%
Apr 19 11:36:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3700.0 ms, Real-time factor: 171.139480
Apr 19 11:36:11 SimulationManager::run [Info]:
Simulation finished.
37.0%
Apr 19 11:36:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3800.0 ms, Real-time factor: 175.338290
Apr 19 11:36:14 SimulationManager::run [Info]:
Simulation finished.
38.0%
Apr 19 11:36:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 3900.0 ms, Real-time factor: 179.436560
Apr 19 11:36:17 SimulationManager::run [Info]:
Simulation finished.
39.0%
Apr 19 11:36:19 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4000.0 ms, Real-time factor: 183.708100
Apr 19 11:36:20 SimulationManager::run [Info]:
Simulation finished.
40.0%
Apr 19 11:36:22 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4100.0 ms, Real-time factor: 187.850330
Apr 19 11:36:23 SimulationManager::run [Info]:
Simulation finished.
41.0%
Apr 19 11:36:25 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4200.0 ms, Real-time factor: 192.070740
Apr 19 11:36:26 SimulationManager::run [Info]:
Simulation finished.
42.0%
Apr 19 11:36:28 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4300.0 ms, Real-time factor: 196.311790
Apr 19 11:36:29 SimulationManager::run [Info]:
Simulation finished.
43.0%
Apr 19 11:36:31 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4400.0 ms, Real-time factor: 200.388120
Apr 19 11:36:31 SimulationManager::run [Info]:
Simulation finished.
44.0%
Apr 19 11:36:34 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4500.0 ms, Real-time factor: 204.522525
Apr 19 11:36:35 SimulationManager::run [Info]:
Simulation finished.
45.0%
Apr 19 11:36:37 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4600.0 ms, Real-time factor: 208.628985
Apr 19 11:36:38 SimulationManager::run [Info]:
Simulation finished.
46.0%
Apr 19 11:36:40 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4700.0 ms, Real-time factor: 212.699730
Apr 19 11:36:41 SimulationManager::run [Info]:
Simulation finished.
47.0%
Apr 19 11:36:43 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4800.0 ms, Real-time factor: 217.743655
Apr 19 11:36:44 SimulationManager::run [Info]:
Simulation finished.
48.0%
Apr 19 11:36:46 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 4900.0 ms, Real-time factor: 221.758590
Apr 19 11:36:47 SimulationManager::run [Info]:
Simulation finished.
49.0%
Apr 19 11:36:49 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5000.0 ms, Real-time factor: 225.805775
Apr 19 11:36:49 SimulationManager::run [Info]:
Simulation finished.
50.0%
Apr 19 11:36:52 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5100.0 ms, Real-time factor: 229.738330
Apr 19 11:36:52 SimulationManager::run [Info]:
Simulation finished.
51.0%
Apr 19 11:36:55 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5200.0 ms, Real-time factor: 233.717475
Apr 19 11:36:55 SimulationManager::run [Info]:
Simulation finished.
52.0%
Apr 19 11:36:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5300.0 ms, Real-time factor: 237.654490
Apr 19 11:36:58 SimulationManager::run [Info]:
Simulation finished.
53.0%
Apr 19 11:37:01 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5400.0 ms, Real-time factor: 241.620775e: 5385.0 ms, Real-time factor: 283.5706
Apr 19 11:37:01 SimulationManager::run [Info]:
Simulation finished.
54.0%
Apr 19 11:37:04 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5500.0 ms, Real-time factor: 245.678255
Apr 19 11:37:04 SimulationManager::run [Info]:
Simulation finished.
55.0%
Apr 19 11:37:07 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5600.0 ms, Real-time factor: 249.818500
Apr 19 11:37:07 SimulationManager::run [Info]:
Simulation finished.
56.0%
Apr 19 11:37:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5700.0 ms, Real-time factor: 254.011505
Apr 19 11:37:10 SimulationManager::run [Info]:
Simulation finished.
57.0%
Apr 19 11:37:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5800.0 ms, Real-time factor: 258.028620
Apr 19 11:37:13 SimulationManager::run [Info]:
Simulation finished.
58.0%
Apr 19 11:37:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 5900.0 ms, Real-time factor: 261.964470
Apr 19 11:37:16 SimulationManager::run [Info]:
Simulation finished.
59.0%
Apr 19 11:37:19 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6000.0 ms, Real-time factor: 265.921750
Apr 19 11:37:19 SimulationManager::run [Info]:
Simulation finished.
60.0%
Apr 19 11:37:22 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6100.0 ms, Real-time factor: 269.958005
Apr 19 11:37:22 SimulationManager::run [Info]:
Simulation finished.
61.0%
Apr 19 11:37:25 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6200.0 ms, Real-time factor: 274.147785
Apr 19 11:37:25 SimulationManager::run [Info]:
Simulation finished.
62.0%
Apr 19 11:37:28 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6300.0 ms, Real-time factor: 278.180890me: 6268.0 ms, Real-time factor: 407.2064
Apr 19 11:37:28 SimulationManager::run [Info]:
Simulation finished.
63.0%
Apr 19 11:37:31 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6400.0 ms, Real-time factor: 282.224865
Apr 19 11:37:31 SimulationManager::run [Info]:
Simulation finished.
64.0%
Apr 19 11:37:34 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6500.0 ms, Real-time factor: 287.381755l time: 6485.0 ms, Real-time factor: 337.1852
Apr 19 11:37:34 SimulationManager::run [Info]:
Simulation finished.
65.0%
Apr 19 11:37:37 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6600.0 ms, Real-time factor: 292.719700
Apr 19 11:37:37 SimulationManager::run [Info]:
Simulation finished.
66.0%
Apr 19 11:37:40 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6700.0 ms, Real-time factor: 297.928300time: 6668.0 ms, Real-time factor: 435.7229
Apr 19 11:37:40 SimulationManager::run [Info]:
Simulation finished.
67.0%
Apr 19 11:37:43 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6800.0 ms, Real-time factor: 303.177260
Apr 19 11:37:44 SimulationManager::run [Info]:
Simulation finished.
68.0%
Apr 19 11:37:46 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 6900.0 ms, Real-time factor: 308.374353odel time: 6885.0 ms, Real-time factor: 361.9108
Apr 19 11:37:47 SimulationManager::run [Info]:
Simulation finished.
69.0%
Apr 19 11:37:49 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7000.0 ms, Real-time factor: 313.505170
Apr 19 11:37:50 SimulationManager::run [Info]:
Simulation finished.
70.0%
Apr 19 11:37:53 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7100.0 ms, Real-time factor: 319.070813
Apr 19 11:37:53 SimulationManager::run [Info]:
Simulation finished.
71.0%
Apr 19 11:37:56 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7200.0 ms, Real-time factor: 323.023983
Apr 19 11:37:56 SimulationManager::run [Info]:
Simulation finished.
72.0%
Apr 19 11:37:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7300.0 ms, Real-time factor: 327.331420
Apr 19 11:37:59 SimulationManager::run [Info]:
Simulation finished.
73.0%
Apr 19 11:38:02 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7400.0 ms, Real-time factor: 332.593820 Model time: 7385.0 ms, Real-time factor: 390.3997
Apr 19 11:38:02 SimulationManager::run [Info]:
Simulation finished.
74.0%
Apr 19 11:38:05 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7500.0 ms, Real-time factor: 336.802090
Apr 19 11:38:05 SimulationManager::run [Info]:
Simulation finished.
75.0%
Apr 19 11:38:08 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7600.0 ms, Real-time factor: 340.891773
Apr 19 11:38:08 SimulationManager::run [Info]:
Simulation finished.
76.0%
Apr 19 11:38:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7700.0 ms, Real-time factor: 345.941543
Apr 19 11:38:11 SimulationManager::run [Info]:
Simulation finished.
77.0%
Apr 19 11:38:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7800.0 ms, Real-time factor: 351.548327Model time: 7768.0 ms, Real-time factor: 514.7829
Apr 19 11:38:15 SimulationManager::run [Info]:
Simulation finished.
78.0%
Apr 19 11:38:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 7900.0 ms, Real-time factor: 356.748190
Apr 19 11:38:18 SimulationManager::run [Info]:
Simulation finished.
79.0%
Apr 19 11:38:20 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8000.0 ms, Real-time factor: 361.131403
Apr 19 11:38:21 SimulationManager::run [Info]:
Simulation finished.
80.0%
Apr 19 11:38:23 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8100.0 ms, Real-time factor: 365.055957
Apr 19 11:38:24 SimulationManager::run [Info]:
Simulation finished.
81.0%
Apr 19 11:38:26 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8200.0 ms, Real-time factor: 369.042590
Apr 19 11:38:27 SimulationManager::run [Info]:
Simulation finished.
82.0%
Apr 19 11:38:29 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8300.0 ms, Real-time factor: 373.174913
Apr 19 11:38:30 SimulationManager::run [Info]:
Simulation finished.
83.0%
Apr 19 11:38:32 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8400.0 ms, Real-time factor: 377.813927
Apr 19 11:38:33 SimulationManager::run [Info]:
Simulation finished.
84.0%
Apr 19 11:38:35 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8500.0 ms, Real-time factor: 381.832757
Apr 19 11:38:36 SimulationManager::run [Info]:
Simulation finished.
85.0%
Apr 19 11:38:38 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8600.0 ms, Real-time factor: 386.786580 85% ] Model time: 8585.0 ms, Real-time factor: 454.1770
Apr 19 11:38:39 SimulationManager::run [Info]:
Simulation finished.
86.0%
Apr 19 11:38:41 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8700.0 ms, Real-time factor: 391.085007
Apr 19 11:38:42 SimulationManager::run [Info]:
Simulation finished.
87.0%
Apr 19 11:38:44 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8800.0 ms, Real-time factor: 395.228320
Apr 19 11:38:45 SimulationManager::run [Info]:
Simulation finished.
88.0%
Apr 19 11:38:47 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 8900.0 ms, Real-time factor: 399.164097
Apr 19 11:38:48 SimulationManager::run [Info]:
Simulation finished.
89.0%
Apr 19 11:38:50 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9000.0 ms, Real-time factor: 403.140237
Apr 19 11:38:51 SimulationManager::run [Info]:
Simulation finished.
90.0%
Apr 19 11:38:53 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9100.0 ms, Real-time factor: 407.147390
Apr 19 11:38:54 SimulationManager::run [Info]:
Simulation finished.
91.0%
Apr 19 11:38:56 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9200.0 ms, Real-time factor: 413.148308
Apr 19 11:38:57 SimulationManager::run [Info]:
Simulation finished.
92.0%
Apr 19 11:38:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9300.0 ms, Real-time factor: 417.084235
Apr 19 11:39:00 SimulationManager::run [Info]:
Simulation finished.
93.0%
Apr 19 11:39:02 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9400.0 ms, Real-time factor: 421.012175
Apr 19 11:39:03 SimulationManager::run [Info]:
Simulation finished.
94.0%
Apr 19 11:39:05 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9500.0 ms, Real-time factor: 425.045858
Apr 19 11:39:06 SimulationManager::run [Info]:
Simulation finished.
95.0%
Apr 19 11:39:08 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9600.0 ms, Real-time factor: 429.079772
Apr 19 11:39:08 SimulationManager::run [Info]:
Simulation finished.
96.0%
Apr 19 11:39:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9700.0 ms, Real-time factor: 433.271405
Apr 19 11:39:11 SimulationManager::run [Info]:
Simulation finished.
97.0%
Apr 19 11:39:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9800.0 ms, Real-time factor: 437.196325
Apr 19 11:39:14 SimulationManager::run [Info]:
Simulation finished.
98.0%
Apr 19 11:39:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 9900.0 ms, Real-time factor: 441.222980
Apr 19 11:39:17 SimulationManager::run [Info]:
Simulation finished.
99.0%
Apr 19 11:39:20 SimulationManager::start_updating_ [Info]:
Number of local nodes: 1087
Simulation time (ms): 100
Number of OpenMP threads: 4
Not using MPI
[ 100% ] Model time: 10000.0 ms, Real-time factor: 445.25468
Apr 19 11:39:20 SimulationManager::run [Info]:
Simulation finished.
Print some network statistics:
[21]:
events_ex = espikes.n_events
events_in = ispikes.n_events
rate_ex = events_ex / total_t_sim * 1000.0 / N_rec
rate_in = events_in / total_t_sim * 1000.0 / N_rec
num_synapses = (nest.GetDefaults("excitatory")["num_connections"] +
nest.GetDefaults("inhibitory")["num_connections"])
print("Balanced network simulation statistics:")
print(f"Number of neurons : {N_neurons}")
print(f"Number of synapses: {num_synapses}")
print(f" Exitatory : {int(CE * N_neurons) + N_neurons}")
print(f" Inhibitory : {int(CI * N_neurons)}")
print(f"Excitatory rate : {rate_ex:.2f} Hz")
print(f"Inhibitory rate : {rate_in:.2f} Hz")
print("Actual times of stimulus presentation: " + str(stim_spikes_rec.events["times"]))
print("Actual t_dopa_spikes = " + str(spikedet_vt.get("events")["times"]))
Balanced network simulation statistics:
Number of neurons : 1000
Number of synapses: 100000
Exitatory : 81000
Inhibitory : 20000
Excitatory rate : 14.43 Hz
Inhibitory rate : 3.42 Hz
Actual times of stimulus presentation: [ 169. 243. 352. 401. 1255. 1285. 1652. 1922. 2243. 2253. 2735. 3230.
3435. 3713. 4081. 4210. 4809. 5582. 6838. 7223. 7274. 8127. 8490. 8677.
8877. 9069. 9634. 9644. 9921. 138. 198. 411. 713. 1859. 2094. 2211.
2676. 2769. 3023. 3041. 3372. 3888. 5491. 5622. 5702. 6041. 6263. 6492.
6755. 6981. 7043. 7473. 8104. 8452. 8746. 9153. 9225. 9434. 9448. 9581.]
Actual t_dopa_spikes = [ 164. 210. 426. 732. 1884. 2107. 2231. 2702. 2786. 3051. 3053. 3396.
3905. 5515. 5634. 5722. 6056. 6291. 6511. 6782. 7000. 7070. 7501. 8127.
8464. 8769. 9165. 9238. 9450. 9460. 9594.]
Rasterplot of network activity
N.B. orange diamonds indicate dopamine spikes.
[22]:
def _histogram(a, bins=10, bin_range=None, normed=False):
"""Calculate histogram for data.
Parameters
----------
a : list
Data to calculate histogram for
bins : int, optional
Number of bins
bin_range : TYPE, optional
Range of bins
normed : bool, optional
Whether distribution should be normalized
Raises
------
ValueError
"""
from numpy import asarray, iterable, linspace, sort, concatenate
a = asarray(a).ravel()
if bin_range is not None:
mn, mx = bin_range
if mn > mx:
raise ValueError("max must be larger than min in range parameter")
if not iterable(bins):
if bin_range is None:
bin_range = (a.min(), a.max())
mn, mx = [mi + 0.0 for mi in bin_range]
if mn == mx:
mn -= 0.5
mx += 0.5
bins = linspace(mn, mx, bins, endpoint=False)
else:
if (bins[1:] - bins[:-1] < 0).any():
raise ValueError("bins must increase monotonically")
# best block size probably depends on processor cache size
block = 65536
n = sort(a[:block]).searchsorted(bins)
for i in range(block, a.size, block):
n += sort(a[i:i + block]).searchsorted(bins)
n = concatenate([n, [len(a)]])
n = n[1:] - n[:-1]
if normed:
db = bins[1] - bins[0]
return 1.0 / (a.size * db) * n, bins
else:
return n, bins
ev = espikes.get("events")
ts, node_ids = ev["times"], ev["senders"]
hist_binwidth = 10. # [ms]
fig, ax = plt.subplots(nrows=2, gridspec_kw={"height_ratios": (2, 1)})
ax[0].plot(ts, node_ids, ".")
ax[0].scatter(t_dopa_spikes, np.zeros_like(t_dopa_spikes), marker="d", c="orange", alpha=.8, zorder=99)
ax[0].set_ylabel("Neuron ID")
t_bins = np.arange(
np.amin(ts), np.amax(ts),
float(hist_binwidth)
)
n, _ = _histogram(ts, bins=t_bins)
num_neurons = len(np.unique(node_ids))
heights = 1000 * n / (hist_binwidth * num_neurons)
ax[1].bar(t_bins, heights, width=hist_binwidth, color="tab:blue", edgecolor="none")
ax[1].set_yticks([
int(x) for x in
np.linspace(0, int(max(heights) * 1.1) + 5, 4)
])
ax[1].set_ylabel("Rate [s${}^{-1}$]")
ax[0].set_xticklabels([])
ax[-1].set_xlabel("Time [ms]")
for _ax in ax:
_ax.set_xlim(0., total_t_sim)
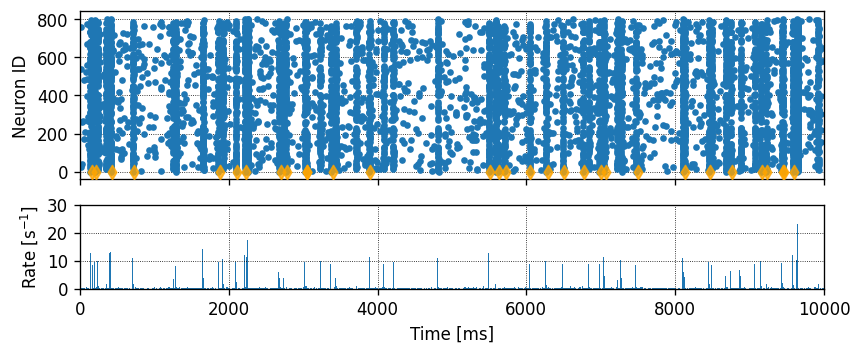
Plot membrane potential of 10 random excitatory cells
This helps to check if the network is in a balanced excitation/inhibition regime.
[23]:
fig, ax = plt.subplots()
for i in range(10):
ax.plot(mms[i].get("events")["times"], mms[i].get("events")["V_m"], label="V_m")
ax.set_xlim(0., total_t_sim)
ax.set_ylabel("$V_m$ [mV]")
ax.set_xlabel("Time [ms]")
None
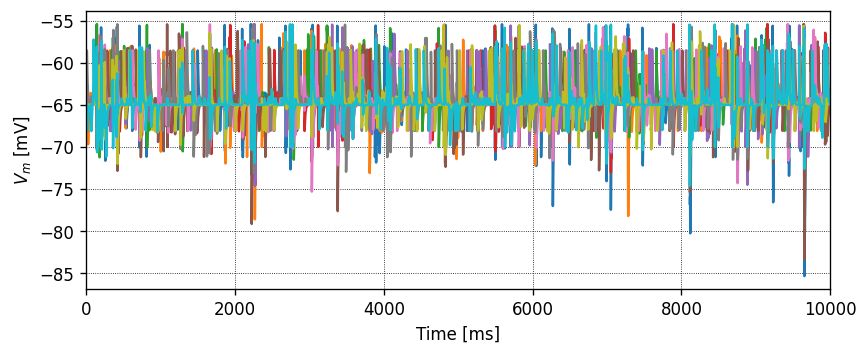
Timeseries
We should verify that the dopamine concentration is the same in group and nongroup neurons.
Note that the timeseries resolution (due to the chunking of the simulation) could be too low to see fast dopamine dynamics. Use more chunks to increase the temporal resolution of this plot, or fewer to speed up the simulation. Consider the relationship between \(\tau_d\) and how many chunks we need to adequately visualize the dynamics.
[24]:
fig,ax = plt.subplots()
ax.plot(log["t"], log["reinforced_group"]["n_avg"], label="avg dopa group", linestyle=":", markersize=10, alpha=.7, marker="x")
ax.plot(log["t"], log["not_reinforced_group"]["n_avg"], label="avg dopa nongroup", linestyle="--", alpha=.7, marker="o")
ax.legend()
ax.set_xlim(0., total_t_sim)
ax.set_xlabel("Time [ms]")
ax.set_ylabel("Dopamine concentration [a.u.]")
None
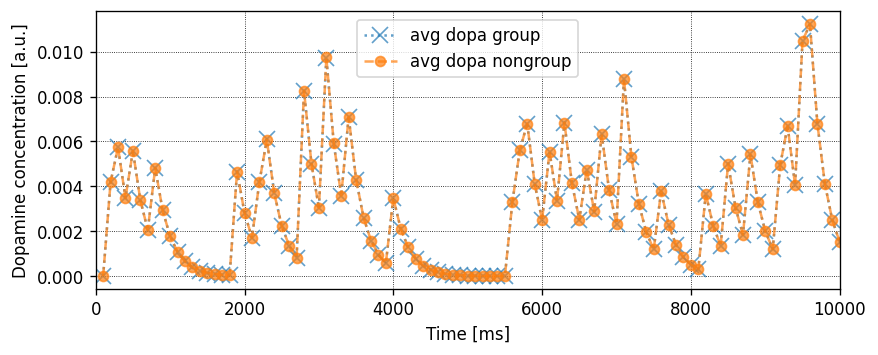
In any case, all synapses seem to be receiving the same dopamine signal.
Now plot the average eligibility trace \(c\) for group and nongroup neurons:
[25]:
fig,ax = plt.subplots(figsize=(8, 3))
ax.plot(log["t"], log["reinforced_group"]["c_sum"], label="group sum")
ax.plot(log["t"], log["not_reinforced_group"]["c_sum"], label="nongroup sum")
ax.scatter(t_dopa_spikes, np.zeros_like(t_dopa_spikes), marker="d", c="orange", alpha=.8, zorder=99)
ax.set_xlim(0., total_t_sim)
ax.set_xlabel("Time [ms]")
ax.set_ylabel("Eligibility trace")
ax.legend()
None
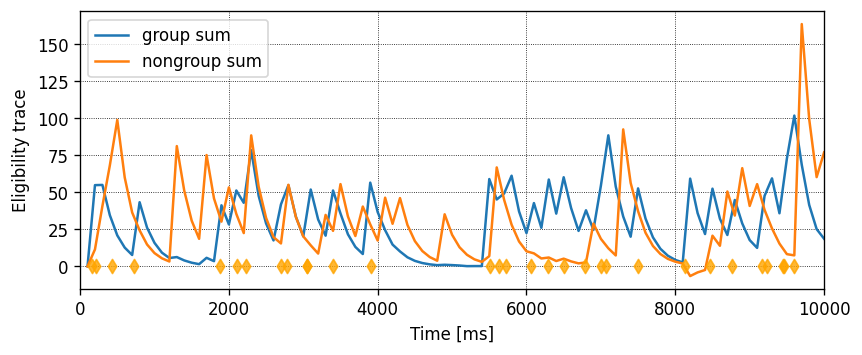
[26]:
fig,ax = plt.subplots(nrows=2, gridspec_kw={"height_ratios": (2, 1)})
ax[0].plot(log["t"], log["reinforced_group"]["w_avg"], label="group")
ax[0].plot(log["t"], log["not_reinforced_group"]["w_avg"], label="nongroup")
ax[0].plot(log["t"], log["w_net"], label="net")
ax[1].plot(log["t"], np.array(log["reinforced_group"]["w_avg"]) - np.array(log["not_reinforced_group"]["w_avg"]),
label="group - nongroup", c="tab:red")
for _ax in ax:
_ax.legend()
_ax.set_xlim(0., total_t_sim)
ax[-1].set_xlabel("Time [ms]")
ax[0].set_xticklabels([])
ax[0].set_ylabel("Average weight ")
None
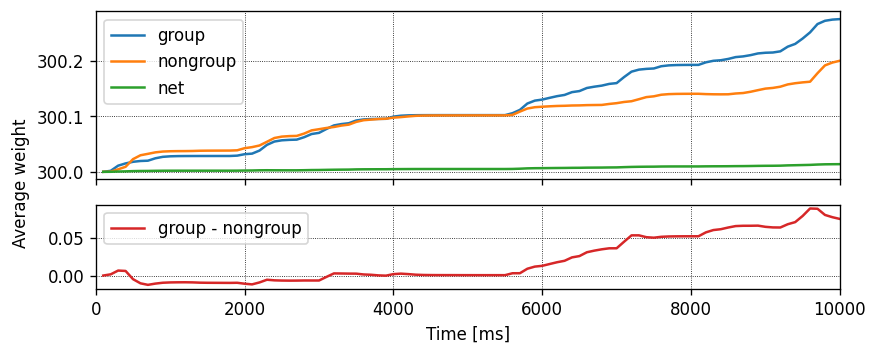
We can also plot all subgroup_size weights over time for the reinforced and non-reinforced groups as a scatterplot.
[27]:
group_weight_times = [[] for _ in range(n_subgroups)]
group_weight_values = [[] for _ in range(n_subgroups)]
senders = np.array(wr.events["senders"])
for subgroup_idx in range(n_subgroups):
nodes_ex_gids = nodes_ex[subgroup_indices[subgroup_idx]].tolist()
idx = [np.where(senders == nodes_ex_gids[i])[0] for i in range(subgroup_size)]
idx = [item for sublist in idx for item in sublist]
group_weight_times[subgroup_idx] = wr.events["times"][idx]
group_weight_values[subgroup_idx] = wr.events["weights"][idx]
fig, ax = plt.subplots()
for subgroup_idx in range(n_subgroups):
if subgroup_idx == reinforced_subgroup_idx:
c = "red"
zorder = 99
marker = "x"
label = "group"
else:
c = "blue"
zorder=1
marker = "o"
label = "nongroup"
ax.scatter(group_weight_times[subgroup_idx], group_weight_values[subgroup_idx], c=c, alpha=.5, zorder=zorder, marker=marker, label=label)
ax.set_ylabel("Weight")
ax.set_xlabel("Time [ms]")
ax.legend()
None
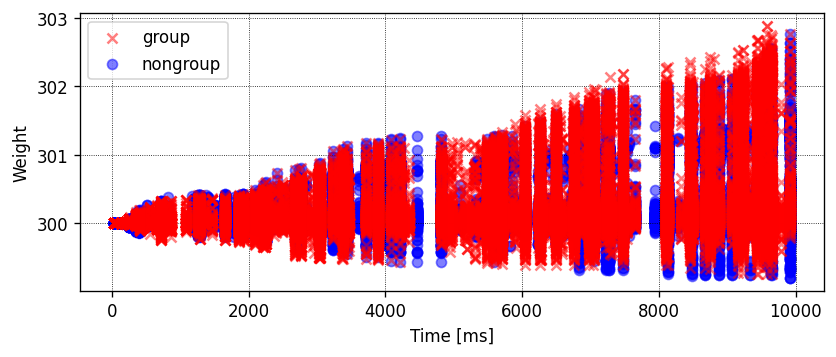
Citations
[1] Mikaitis M, Pineda García G, Knight JC and Furber SB (2018) Neuromodulated Synaptic Plasticity on the SpiNNaker Neuromorphic System. Front. Neurosci. 12:105. doi: 10.3389/fnins.2018.00105
[2] PyGeNN: A Python library for GPU-enhanced neural networks, James C. Knight, Anton Komissarov, Thomas Nowotny. Frontiers
[3] Eugene M. Izhikevich. Solving the distal reward problem through linkage of STDP and dopamine signaling. Cerebral Cortex 17, no. 10 (2007): 2443-2452.
[4] Nicolas Brunel. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. Journal of Computational Neuroscience 8(3):183-208 (2000)
Acknowledgements
This software was developed in part or in whole in the Human Brain Project, funded from the European Union’s Horizon 2020 Framework Programme for Research and Innovation under Specific Grant Agreements No. 720270, No. 785907 and No. 945539 (Human Brain Project SGA1, SGA2 and SGA3).
The authors would like to thank James Knight, Garibaldi García and Mantas Mikaitis for their kind and helpful feedback.
License
This notebook (and associated files) is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 2 of the License, or (at your option) any later version.
This notebook (and associated files) is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.