NESTML spike frequency adaptation tutorial
Welcome to the NESTML spike frequency adaptation (SFA) tutorial. Here, we will go step by step through adding two different types of SFA mechanism to a neuron model, threshold adaptation and an adaptation current [1], and then evaluate how the new models behave in simulation.
Table of contents
Introduction
A neuron that is stimulated by rectangular current injections initially responds with a high firing rate, followed by a decrease in the firing rate. This phenomenon is called spike-frequency adaptation and is usually mediated by slow K+ currents, such as a Ca2+-activated K+ current [3]. This behaviour is typically modelled in one of two ways:
Threshold adaptation: The threshold for generating an action potential is increased every time an action potential occurs. The threshold slowly decays back to its original value.
Potassium membrane current: An extra transmembrane current is added to the neuron, that is increased step-wise every time an action potential occurs, and slowly decays back to its original value.
Quiz: If a typical point neuron model has a characteristic timescale (in its membrane potential dynamics) of 20 ms, what would be good order-of-magnitude estimate to give to the adaptation characteristic timescale? How does refractoriness figure into this?
Solution: Considerably longer than the neuron timescale, e.g. 200 ms; refractoriness defines a maximum neuron firing rate; consider maximum and minimum obtained firing rates in the presence of the SFA mechanism.
[1]:
%matplotlib inline
from typing import List, Optional
import matplotlib as mpl
mpl.rcParams['axes.formatter.useoffset'] = False
mpl.rcParams['axes.grid'] = True
mpl.rcParams['grid.color'] = 'k'
mpl.rcParams['grid.linestyle'] = ':'
mpl.rcParams['grid.linewidth'] = 0.5
mpl.rcParams['figure.dpi'] = 120
mpl.rcParams['figure.figsize'] = [8., 3.]
import matplotlib.pyplot as plt
import nest
import numpy as np
import os
import random
import re
import uuid
from pynestml.codegeneration.nest_code_generator_utils import NESTCodeGeneratorUtils
/home/charl/.local/lib/python3.11/site-packages/matplotlib/projections/__init__.py:63: UserWarning: Unable to import Axes3D. This may be due to multiple versions of Matplotlib being installed (e.g. as a system package and as a pip package). As a result, the 3D projection is not available.
warnings.warn("Unable to import Axes3D. This may be due to multiple versions of "
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
Generating code with NESTML
We will take a simple current-based integrate-and-fire model with alpha-shaped postsynaptic response kernels (iaf_psc_alpha) as the basis for our modifications. First, let’s take a look at this base neuron without any modifications.
We will use a helper function to generate the C++ code for the models, build it as a NEST extension module, and load the module into the kernel. Because NEST does not support un- or reloading of modules at the time of writing, we implement a workaround that appends a unique number to the name of each generated model, for example, “iaf_psc_alpha_3cc945f”. The resulting neuron model name is returned by the function, so we do not have to think about these internals.
Base model: no adaptation
Let’s first make sure that we have all the necessary files.
If you are running this notebook locally or cloned the repository, the NESTML model iaf_psc_alpha_neuron.nestml is contained in the subdirectory models. You can open NESTML model files in your favourite code editor (check https://github.com/nest/nestml/ for syntax highlighting support). In case you are running this notebook in JupyerLab, you can edit the model files directly in your browser via the “File browser” panel on the left.
[2]:
# generate and build code
module_name_no_sfa, neuron_model_name_no_sfa = \
NESTCodeGeneratorUtils.generate_code_for("models/iaf_psc_alpha.nestml")
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
WARNING:Under certain conditions, the propagator matrix is singular (contains infinities).
WARNING:List of all conditions that result in a singular propagator:
WARNING: tau_m = tau_syn_inh
WARNING: tau_m = tau_syn_exc
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
CMake Warning (dev) at CMakeLists.txt:93 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
nestml_4e02d9e66e71411b95e21d3a31d61a56_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'nestml_4e02d9e66e71411b95e21d3a31d61a56_module' using
make
make install
The library file libnestml_4e02d9e66e71411b95e21d3a31d61a56_module.so will be installed to
/tmp/nestml_target_gw9m9vvq
The module can be loaded into NEST using
(nestml_4e02d9e66e71411b95e21d3a31d61a56_module) Install (in SLI)
nest.Install(nestml_4e02d9e66e71411b95e21d3a31d61a56_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target
[ 33%] Building CXX object CMakeFiles/nestml_4e02d9e66e71411b95e21d3a31d61a56_module_module.dir/nestml_4e02d9e66e71411b95e21d3a31d61a56_module.o
[ 66%] Building CXX object CMakeFiles/nestml_4e02d9e66e71411b95e21d3a31d61a56_module_module.dir/iaf_psc_alpha_neuron_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_neuron_nestml.cpp: In member function ‘void iaf_psc_alpha_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_neuron_nestml.cpp:198:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
198 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_alpha_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_neuron_nestml.cpp:319:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
319 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_neuron_nestml.cpp:314:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
314 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
[100%] Linking CXX shared module nestml_4e02d9e66e71411b95e21d3a31d61a56_module.so
[100%] Built target nestml_4e02d9e66e71411b95e21d3a31d61a56_module_module
[100%] Built target nestml_4e02d9e66e71411b95e21d3a31d61a56_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_gw9m9vvq/nestml_4e02d9e66e71411b95e21d3a31d61a56_module.so
Now, the NESTML model is ready to be used in a simulation.
[3]:
def evaluate_neuron(neuron_name, module_name, neuron_parms=None, stimulus_type="constant",
mu=500., sigma=0., t_sim=300., plot=True):
"""
Run a simulation in NEST for the specified neuron. Inject a stepwise
current and plot the membrane potential dynamics and spikes generated.
"""
dt = .1 # [ms]
nest.ResetKernel()
nest.Install(module_name)
neuron = nest.Create(neuron_name)
if neuron_parms:
for k, v in neuron_parms.items():
nest.SetStatus(neuron, k, v)
if stimulus_type == "constant":
nest.SetStatus(neuron, "I_e", mu)
assert sigma == 0.
elif stimulus_type == "Ornstein-Uhlenbeck":
nest.SetStatus(neuron, "I_noise0", mu)
nest.SetStatus(neuron, "sigma_noise", sigma)
else:
raise Exception("Unknown stimulus type: " + str(stimulus_type))
multimeter = nest.Create("multimeter")
multimeter.set({"record_from": ["V_m"],
"interval": dt})
spike_recorder = nest.Create("spike_recorder")
nest.Connect(multimeter, neuron)
nest.Connect(neuron, spike_recorder)
nest.Simulate(t_sim)
dmm = nest.GetStatus(multimeter)[0]
Voltages = dmm["events"]["V_m"]
tv = dmm["events"]["times"]
dSD = nest.GetStatus(spike_recorder, keys='events')[0]
spikes = dSD['senders']
ts = dSD["times"]
_idx = [np.argmin((tv - spike_time)**2) - 1 for spike_time in ts]
V_m_at_spike_times = Voltages[_idx]
if plot:
fig, ax = plt.subplots()
ax.plot(tv, Voltages)
ax.scatter(ts, V_m_at_spike_times)
ax.set_xlabel("Time [ms]")
ax.set_ylabel("V_m [mV]")
ax.grid()
return ts
[4]:
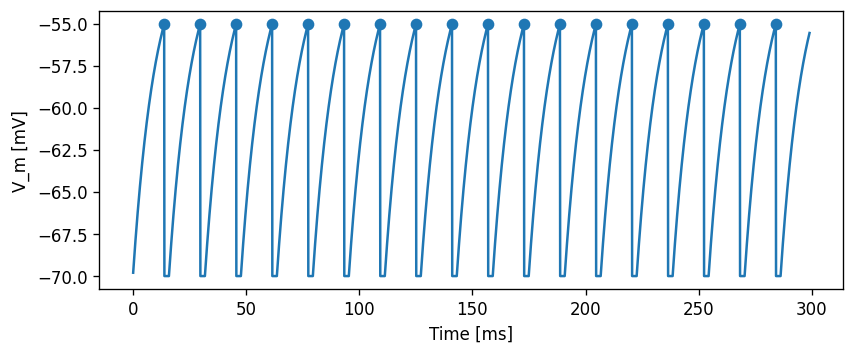
evaluate_neuron(neuron_model_name_no_sfa, module_name_no_sfa)
Apr 19 11:10:06 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:10:06 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:10:06 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 300
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:10:06 SimulationManager::run [Info]:
Simulation finished.
[4]:
array([ 13.9, 29.8, 45.7, 61.6, 77.5, 93.4, 109.3, 125.2, 141.1,
157. , 172.9, 188.8, 204.7, 220.6, 236.5, 252.4, 268.3, 284.2])
Current-based adaptation
Specifically incorporate an adaptation current \(I_{sfa}(t)\) while keeping the firing threshold constant. The current will always be non-negative, and is set up so that the current will hyperpolarise the neuron. The dynamical system model is adjusted in this case to
\begin{align} \frac{dV_m}{dt} &= (I_{syn} + I_{ext} - I_{sfa}) / \tau_m\\ \frac{dI_{sfa}}{dt} &= -I_{sfa} / \tau_{sfa} \end{align}
where \(I_{sfa}\) is instantaneously increased by \(\Delta{}I_{sfa}\) at each the neuron fires and \(\tau_{sfa}\) controls the decay rate for the adaptation current.
Adjusting the NESTML model
Task: Create a new file and name it, for example, iaf_psc_alpha_adapt_curr.nestml. Copy the contents of iaf_psc_alpha_neuron.nestml and make the following changes.
First, define the parameters:
parameters:
[...]
tau_sfa ms = 100 ms
Delta_I_sfa pA = 100 pA
Add the new state variables and initial values:
state:
[...]
I_sfa pA = 0 pA
equations:
[...]
I_sfa' = -I_sfa / tau_sra
and add the new term to the dynamical equation for V_m:
equations:
[...]
function I pA = convolve(I_shape_in, in_spikes) + convolve(I_shape_ex, ex_spikes) - I_sfa + I_e + I_stim
V_m' = -(V_m - E_L) / Tau + I / C_m
Increment the adaptation current whenever the neuron fires:
onCondition(V_m >= Theta):
[...]
I_sfa += Delta_I_sfa
emit_spike()
[5]:
# generate and build code
module_name_adapt_curr, neuron_model_name_adapt_curr = \
NESTCodeGeneratorUtils.generate_code_for("models/iaf_psc_alpha_adapt_curr.nestml")
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
WARNING:Under certain conditions, the propagator matrix is singular (contains infinities).
WARNING:List of all conditions that result in a singular propagator:
WARNING: tau_m = tau_sfa
WARNING: tau_m = tau_syn_inh
WARNING: tau_m = tau_syn_exc
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
WARNING:Not preserving expression for variable "I_sfa" as it is solved by propagator solver
CMake Warning (dev) at CMakeLists.txt:93 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
nestml_9c5da0c0943741c7b8b8c6f3f2696680_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'nestml_9c5da0c0943741c7b8b8c6f3f2696680_module' using
make
make install
The library file libnestml_9c5da0c0943741c7b8b8c6f3f2696680_module.so will be installed to
/tmp/nestml_target_tl2yd4po
The module can be loaded into NEST using
(nestml_9c5da0c0943741c7b8b8c6f3f2696680_module) Install (in SLI)
nest.Install(nestml_9c5da0c0943741c7b8b8c6f3f2696680_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target
[ 33%] Building CXX object CMakeFiles/nestml_9c5da0c0943741c7b8b8c6f3f2696680_module_module.dir/nestml_9c5da0c0943741c7b8b8c6f3f2696680_module.o
[ 66%] Building CXX object CMakeFiles/nestml_9c5da0c0943741c7b8b8c6f3f2696680_module_module.dir/iaf_psc_alpha_adapt_curr_neuron_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_curr_neuron_nestml.cpp: In member function ‘void iaf_psc_alpha_adapt_curr_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_curr_neuron_nestml.cpp:204:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
204 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_curr_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_alpha_adapt_curr_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_curr_neuron_nestml.cpp:332:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
332 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_curr_neuron_nestml.cpp:327:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
327 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
[100%] Linking CXX shared module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module.so
[100%] Built target nestml_9c5da0c0943741c7b8b8c6f3f2696680_module_module
[100%] Built target nestml_9c5da0c0943741c7b8b8c6f3f2696680_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_tl2yd4po/nestml_9c5da0c0943741c7b8b8c6f3f2696680_module.so
[6]:
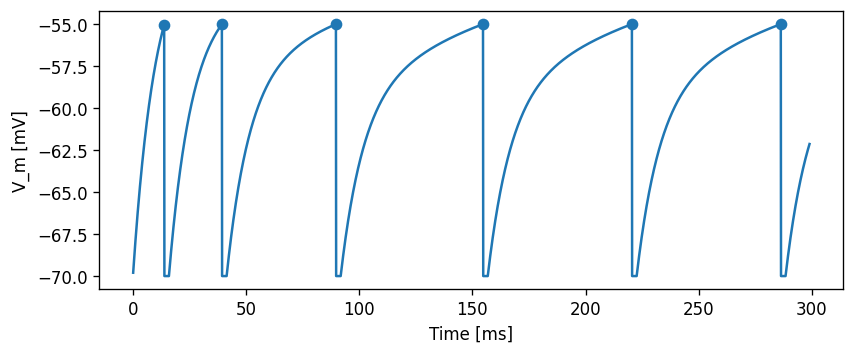
evaluate_neuron(neuron_model_name_adapt_curr, module_name_adapt_curr)
Apr 19 11:11:02 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:11:02 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:11:02 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 300
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:11:02 SimulationManager::run [Info]:
Simulation finished.
[6]:
array([ 13.9, 39.4, 89.8, 154.8, 220.6, 286.4])
Task: Record and plot the adaptation current \(I_{sfa}\).
Threshold-based adaptation
We reflect spike-frequency adaptation by increasing the firing threshold \(\Theta\) by \(\Delta\Theta\) the moment the neuron fires. Between firing events, \(\Theta\) evolves according to
\begin{align} \frac{d\Theta}{dt} &= -(\Theta - \Theta_{init}) / \tau_\Theta \end{align}
such that the firing threshold decays to the constant non-adapted firing threshold, in the absence of firing events, and \(\tau_\Theta\) determines the decay rate.
Task: As for the threshold adaptation case, create a new model file and make the necessary adjustments.
[7]:
# generate and build code
module_name_adapt_thresh, neuron_model_name_adapt_thresh = \
NESTCodeGeneratorUtils.generate_code_for("models/iaf_psc_alpha_adapt_thresh.nestml")
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
WARNING:Under certain conditions, the propagator matrix is singular (contains infinities).
WARNING:List of all conditions that result in a singular propagator:
WARNING: tau_m = tau_syn_inh
WARNING: tau_m = tau_syn_exc
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
WARNING:Not preserving expression for variable "Theta" as it is solved by propagator solver
CMake Warning (dev) at CMakeLists.txt:93 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module' using
make
make install
The library file libnestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module.so will be installed to
/tmp/nestml_target_2p4fhhc6
The module can be loaded into NEST using
(nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module) Install (in SLI)
nest.Install(nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target
[ 33%] Building CXX object CMakeFiles/nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module_module.dir/nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module.o
[ 66%] Building CXX object CMakeFiles/nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module_module.dir/iaf_psc_alpha_adapt_thresh_neuron_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_neuron_nestml.cpp: In member function ‘void iaf_psc_alpha_adapt_thresh_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_neuron_nestml.cpp:203:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
203 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_alpha_adapt_thresh_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_neuron_nestml.cpp:329:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
329 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_neuron_nestml.cpp:324:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
324 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
[100%] Linking CXX shared module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module.so
[100%] Built target nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module_module
[100%] Built target nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_2p4fhhc6/nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module.so
[8]:
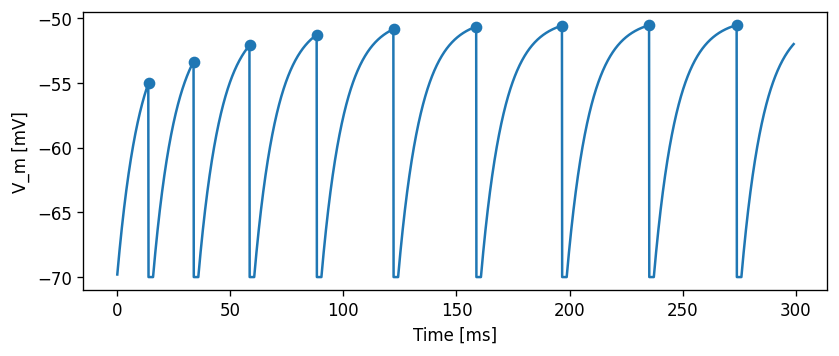
evaluate_neuron(neuron_model_name_adapt_thresh, module_name_adapt_thresh)
Apr 19 11:11:53 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:11:53 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:11:53 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 300
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:11:53 SimulationManager::run [Info]:
Simulation finished.
[8]:
array([ 13.9, 33.9, 58.6, 88.3, 122.2, 158.8, 196.7, 235.2, 273.9])
Slope-dependent threshold
As an extra challenge: implement the slope-dependent threshold from https://www.pnas.org/content/97/14/8110
Characterisation
We now use various metrics to quantify and compare the behavior of the different neuron model variants.
f-I curve
[9]:
def measure_fI_curve(I_stim_vec, neuron_model_name, module_name):
r"""For a range of stimulation currents ``I_stim_vec``, measure the steady
state firing rate of the neuron ``neuron_model_name`` and return them as a
vector ``rate_testant`` of the same size as ``I_stim_vec``."""
t_stop = 10000. # simulate for a long time to make any startup transients insignificant [ms]
rate_testant = float("nan") * np.ones_like(I_stim_vec)
for i, I_stim in enumerate(I_stim_vec):
nest.ResetKernel()
nest.Install(module_name)
neuron = nest.Create(neuron_model_name)
dc = nest.Create("dc_generator", params={"amplitude": I_stim * 1E12}) # 1E12: convert A to pA
nest.Connect(dc, neuron)
sr_testant = nest.Create('spike_recorder')
nest.Connect(neuron, sr_testant)
nest.Simulate(t_stop)
rate_testant[i] = sr_testant.n_events / t_stop * 1000
return rate_testant
[10]:
def plot_fI_curve(I_stim_vec, label_to_rate_vec):
if len(I_stim_vec) < 40:
marker = "o"
else:
marker = None
fig, ax = plt.subplots()
ax = [ax]
for label, rate_vec in label_to_rate_vec.items():
ax[0].plot(I_stim_vec * 1E12, rate_vec, marker=marker, label=label)
for _ax in ax:
_ax.legend(loc='upper right')
_ax.grid()
_ax.set_ylabel("Firing rate [Hz]")
ax[0].set_xlabel("$I_{inj}$ [pA]")
plt.tight_layout()
[12]:
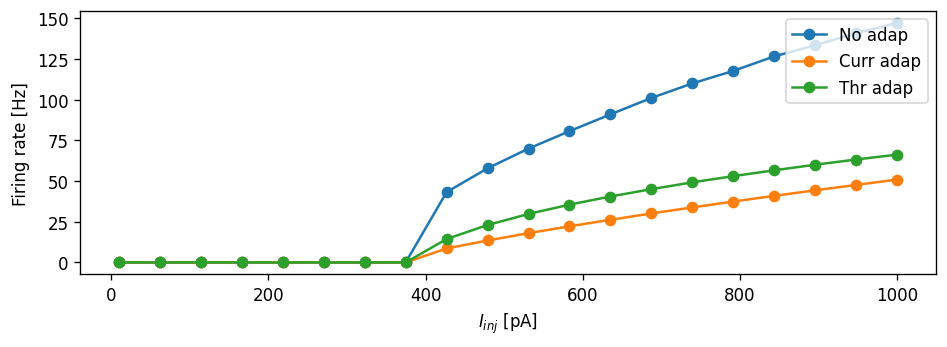
I_stim_vec = np.linspace(10E-12, 1E-9, 20) # [A]
rate_vec = measure_fI_curve(I_stim_vec, neuron_model_name_no_sfa, module_name_no_sfa)
rate_vec_adapt = measure_fI_curve(I_stim_vec, neuron_model_name_adapt_curr, module_name_adapt_curr)
rate_vec_thresh_adapt = measure_fI_curve(I_stim_vec, neuron_model_name_adapt_thresh, module_name_adapt_thresh)
plot_fI_curve(I_stim_vec, {"No adap": rate_vec,
"Curr adap" : rate_vec_adapt,
"Thr adap" : rate_vec_thresh_adapt})
Apr 19 11:16:10 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:10 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:10 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:10 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:10 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:10 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:10 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:10 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:11 Install [Info]:
loaded module nestml_4e02d9e66e71411b95e21d3a31d61a56_module
Apr 19 11:16:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:12 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_9c5da0c0943741c7b8b8c6f3f2696680_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:13 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:13 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:16:14 Install [Info]:
loaded module nestml_0caaf47dae6c4cb6bdf8977ac5d3c855_module
Apr 19 11:16:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:16:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:16:14 SimulationManager::run [Info]:
Simulation finished.
Task: Can you make the current adaptation model curve and threshold adaptation curve overlap? Can you do this without re-generating the NESTML models?
CV vs. firing rate
The Ornstein-Uhlenbeck process is often used as a source of noise because it is well understood and has convenient properties (it is a Gaussian process, has the Markov property, and is stationary). Let the O-U process, denoted \(U(t)\) (with \(t\geq 0\)) , be defined as the solution of the following stochastic differential equation:
\begin{align} \frac{dU}{dt} = \frac{\mu - U}{\tau} + \sigma\sqrt{\frac 2 \tau} \frac{dB(t)}{dt} \end{align}
The first right-hand side term is a “drift” term which is deterministic and slowly reverts \(U_t\) to the mean \(\mu\), with time constant \(\tau\). The second term is stochastic as \(B(t)\) is the Brownian motion (also “Wiener”) process, and \(\sigma>0\) is the standard deviation of the noise.
It turns out that the infinitesimal step in Brownian motion is white noise, that is, an independent and identically distributed sequence of Gaussian \(\mathcal{N}(0, 1)\) random variables. The noise \(dB(t)/dt\) can be sampled at time \(t\) by drawing a sample from that Gaussian distribution, so if the process is sampled at discrete intervals of length \(h\), we can write (equation 2.47 from [1]):
\begin{align} U(t + h) = (U(t) - \mu)\exp(-h/\tau) + \sigma\sqrt{(1 - \exp(-2h / \tau ))} \cdot\mathcal{N}(0, 1) \end{align}
We can write this in NESTML as:
parameters:
I_noise0 pA = 500 pA # mean of the noise current
sigma_noise pA = 50 pA # std. dev. of the noise current
internals:
[...]
D_noise pA**2/ms = 2 * sigma_noise**2 / tau_syn
A_noise pA = ((D_noise * tau_syn / 2) * (1 - exp(-2 * resolution() / tau_syn )))**.5
state:
I_noise pA = I_noise0
update:
[...]
I_noise = I_noise0
+ (I_noise - I_noise0) * exp(-resolution() / tau_syn)
+ A_noise * random_normal(0, 1)
[13]:
# generate and build code
module_name_adapt_thresh_ou, neuron_model_name_adapt_thresh_ou = \
NESTCodeGeneratorUtils.generate_code_for("models/iaf_psc_alpha_adapt_thresh_OU.nestml")
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
WARNING:Under certain conditions, the propagator matrix is singular (contains infinities).
WARNING:List of all conditions that result in a singular propagator:
WARNING: tau_m = tau_syn_exc
WARNING: tau_m = tau_syn_inh
WARNING:Not preserving expression for variable "V_m" as it is solved by propagator solver
WARNING:Not preserving expression for variable "Theta" as it is solved by propagator solver
CMake Warning (dev) at CMakeLists.txt:93 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
nestml_db743385b3864e6e9f1eb9b781769b0e_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'nestml_db743385b3864e6e9f1eb9b781769b0e_module' using
make
make install
The library file libnestml_db743385b3864e6e9f1eb9b781769b0e_module.so will be installed to
/tmp/nestml_target_66ed1u9x
The module can be loaded into NEST using
(nestml_db743385b3864e6e9f1eb9b781769b0e_module) Install (in SLI)
nest.Install(nestml_db743385b3864e6e9f1eb9b781769b0e_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target
[ 33%] Building CXX object CMakeFiles/nestml_db743385b3864e6e9f1eb9b781769b0e_module_module.dir/nestml_db743385b3864e6e9f1eb9b781769b0e_module.o
[ 66%] Building CXX object CMakeFiles/nestml_db743385b3864e6e9f1eb9b781769b0e_module_module.dir/iaf_psc_alpha_adapt_thresh_OU_neuron_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_OU_neuron_nestml.cpp: In member function ‘void iaf_psc_alpha_adapt_thresh_OU_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_OU_neuron_nestml.cpp:209:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
209 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_OU_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_alpha_adapt_thresh_OU_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_OU_neuron_nestml.cpp:342:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
342 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/spike_frequency_adaptation/target/iaf_psc_alpha_adapt_thresh_OU_neuron_nestml.cpp:337:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
337 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
[100%] Linking CXX shared module nestml_db743385b3864e6e9f1eb9b781769b0e_module.so
[100%] Built target nestml_db743385b3864e6e9f1eb9b781769b0e_module_module
[100%] Built target nestml_db743385b3864e6e9f1eb9b781769b0e_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_66ed1u9x/nestml_db743385b3864e6e9f1eb9b781769b0e_module.so
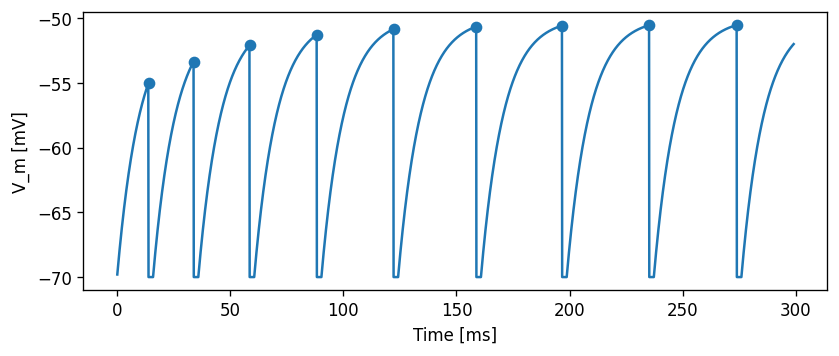
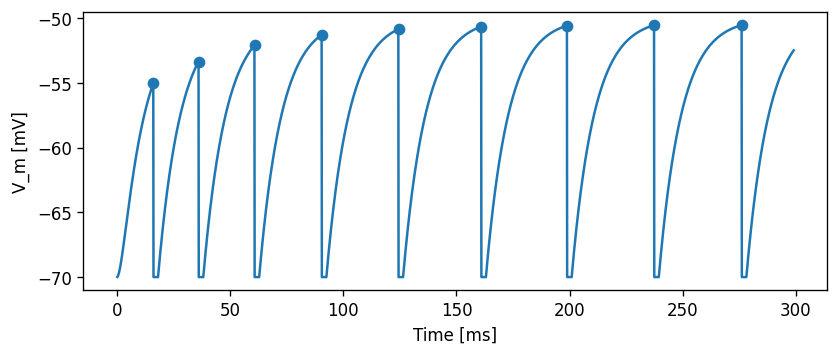
Let’s first do some sanity check that our model is behaving as expected. If we set \(\sigma\) to zero, the response should match the one for the constant current input, so the following two plots should look exactly the same:
[14]:
evaluate_neuron(neuron_model_name_adapt_thresh_ou,
module_name_adapt_thresh_ou,
stimulus_type="constant",
mu=500.)
evaluate_neuron(neuron_model_name_adapt_thresh_ou,
module_name_adapt_thresh_ou,
stimulus_type="Ornstein-Uhlenbeck",
mu=500.,
sigma=0.)
Apr 19 11:17:12 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 300
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:12 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 300
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:12 SimulationManager::run [Info]:
Simulation finished.
[14]:
array([ 16.1, 36.1, 60.8, 90.5, 124.4, 161. , 198.9, 237.4, 276.1])
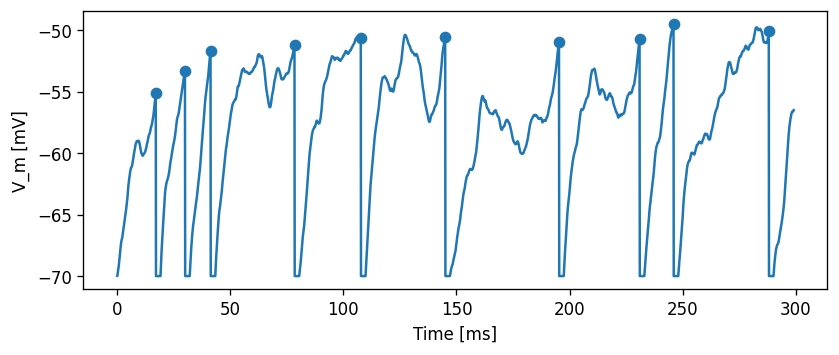
Now, for the same \(\mu\)=500 pA, but setting \(\sigma\)=200 pA/√ms, the effect of the noise can be clearly seen in the membrane potential trace and in the spiking irregularity:
[15]:
spike_times = evaluate_neuron(neuron_model_name_adapt_thresh_ou,
module_name_adapt_thresh_ou,
stimulus_type="Ornstein-Uhlenbeck",
mu=500.,
sigma=200.)
Apr 19 11:17:13 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 300
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:13 SimulationManager::run [Info]:
Simulation finished.
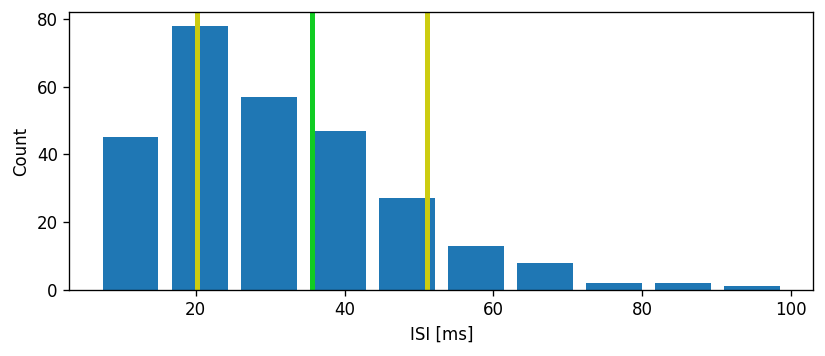
Let’s first do a sanity check and plot a distribution of the interspike intervals, as well as their mean and standard deviation interval.
[16]:
spike_times = evaluate_neuron(neuron_model_name_adapt_thresh_ou,
module_name_adapt_thresh_ou,
stimulus_type="Ornstein-Uhlenbeck",
mu=500.,
sigma=200.,
t_sim=10000.,
plot=False)
ISI = np.diff(spike_times)
ISI_mean = np.mean(ISI)
ISI_std = np.std(ISI)
print("Mean: " + str(ISI_mean))
print("Std. dev.: " + str(ISI_std))
count, bin_edges = np.histogram(ISI)
fig, ax = plt.subplots()
ax.bar(bin_edges[:-1], count, width=.8 * (bin_edges[1] - bin_edges[0]))
ylim = ax.get_ylim()
ax.plot([ISI_mean, ISI_mean], ax.get_ylim(), c="#11CC22", linewidth=3)
ax.plot([ISI_mean - ISI_std, ISI_mean - ISI_std], ylim, c="#CCCC11", linewidth=3)
ax.plot([ISI_mean + ISI_std, ISI_mean + ISI_std], ylim, c="#CCCC11", linewidth=3)
ax.set_ylim(ylim)
ax.set_xlabel("ISI [ms]")
ax.set_ylabel("Count")
ax.grid()
Apr 19 11:17:13 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 10000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:13 SimulationManager::run [Info]:
Simulation finished.
Mean: 35.57857142857143
Std. dev.: 15.445684953198752
Task: The CV is defined as the standard deviation of the ISIs divided by the mean:
\begin{align} CV = \frac{\sigma}{\mu} \end{align}
Comment on whether the coefficient of variation is an appropriate metric to use.
Now, we can use the ISIs to calculate the coefficient of variation. Sanity check: Poisson process should have CV = 1 irrespective of the rate.
[17]:
mean_interval = 1.
isi = np.random.exponential(mean_interval, 1000)
print("For a Poisson process:")
print("CV = " + str(np.std(isi) / np.mean(isi)))
For a Poisson process:
CV = 0.9595231331304875
[18]:
CV = np.std(ISI) / np.mean(ISI)
print("CV: " + str(np.std(ISI) / np.mean(ISI)))
CV: 0.4341288683894449
Let’s compute the CV across a range of input currents and compare this to the non-adapting model:
[19]:
def cv_across_curr(neuron_model_name, module_name, neuron_params, N=40):
t_sim = 25E3 # [ms]
CV = np.nan * np.ones(N)
rate = np.nan * np.ones(N)
for i, mu in enumerate(np.logspace(np.log10(150.), np.log10(700.), N)):
spike_times = evaluate_neuron(neuron_model_name,
module_name=module_name,
stimulus_type="Ornstein-Uhlenbeck",
mu=mu,
sigma=100.,
t_sim=t_sim,
plot=False,
neuron_parms=neuron_params)
rate[i] = len(spike_times) / (t_sim / 1E3)
ISI = np.diff(spike_times)
if len(ISI) > 0:
ISI_mean = np.mean(ISI)
ISI_std = np.std(ISI)
CV[i] = ISI_std / ISI_mean
return CV, rate
[20]:
CV_reg, rate_reg = cv_across_curr(neuron_model_name_adapt_thresh_ou,
module_name_adapt_thresh_ou,
{"Delta_Theta" : 0.})
CV_adapt, rate_adapt = cv_across_curr(neuron_model_name_adapt_thresh_ou,
module_name_adapt_thresh_ou,
{"Delta_Theta" : 5.})
fig, ax = plt.subplots()
ax.scatter(rate_reg, CV_reg, label="non-adapt")
ax.scatter(rate_adapt, CV_adapt, color="orange", label="adapt")
ax.set_xlabel("Firing rate [1/s]")
ax.set_ylabel("CV")
ax.legend()
ax.grid()
Apr 19 11:17:14 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:14 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:14 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:14 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:14 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:14 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:14 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:15 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:15 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:15 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:15 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:15 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:15 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:15 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:15 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:15 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:15 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:15 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:15 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:15 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:15 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:16 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:16 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:16 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:16 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:16 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:16 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:16 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:16 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:16 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:16 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:16 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:16 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:16 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:16 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:17 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:17 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:17 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:17 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:17 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:17 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:17 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:17 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:18 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:18 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:18 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:18 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:18 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:18 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:19 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:19 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:19 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:19 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:19 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:19 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:19 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:19 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:20 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:20 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:20 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:20 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:21 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:21 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:21 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:21 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:22 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:22 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:22 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:22 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:23 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:23 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:23 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:23 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:25 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:25 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:25 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:25 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:26 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:26 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:26 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:26 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:28 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:28 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:28 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:28 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:30 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:30 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:30 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:30 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:32 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:32 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:32 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:32 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:34 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:34 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:34 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:34 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:36 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:36 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:36 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:36 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:39 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:39 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:39 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:39 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:41 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:41 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:41 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:41 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:44 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:44 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:44 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:44 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:47 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:47 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:47 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:47 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:50 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:50 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:50 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:50 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:53 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:53 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:53 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:53 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:57 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:57 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:57 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:57 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:57 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:57 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:57 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:57 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:57 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:57 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:57 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:57 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:57 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:57 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:57 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:57 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:57 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:57 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:57 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:57 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:57 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:57 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:57 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:58 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:58 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:58 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:58 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:58 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:58 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:58 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:58 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:58 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:58 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:58 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:58 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:58 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:58 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:58 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:58 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:59 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:59 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:59 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:59 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:59 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:59 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:59 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:59 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:59 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:59 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:59 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:59 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:59 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:17:59 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:17:59 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:17:59 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:17:59 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:00 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:00 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:00 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:00 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:00 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:00 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:00 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:00 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:00 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:00 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:00 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:00 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:00 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:00 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:00 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:00 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:01 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:01 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:01 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:01 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:01 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:01 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:01 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:01 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:01 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:01 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:01 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:01 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:02 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:02 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:02 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:02 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:02 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:02 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:02 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:02 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:02 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:02 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:02 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:03 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:03 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:03 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:03 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:03 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:03 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:03 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:03 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:04 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:04 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:04 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:04 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:04 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:05 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:05 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:05 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:05 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:05 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:05 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:05 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:05 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:06 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:06 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:06 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:06 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:07 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:07 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:07 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:07 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:07 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:07 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:07 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:07 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:08 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:08 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:08 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:08 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:09 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:09 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:09 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:09 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:10 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:10 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:10 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:10 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:11 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:11 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:11 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:11 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:12 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:12 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:12 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:12 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:18:13 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:18:13 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:18:13 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 25000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:18:13 SimulationManager::run [Info]:
Simulation finished.
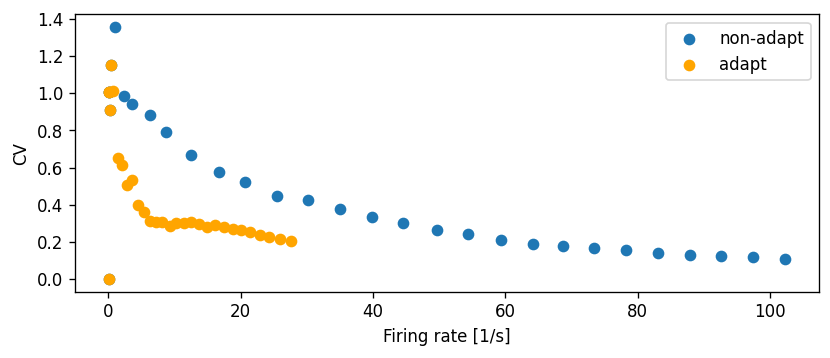
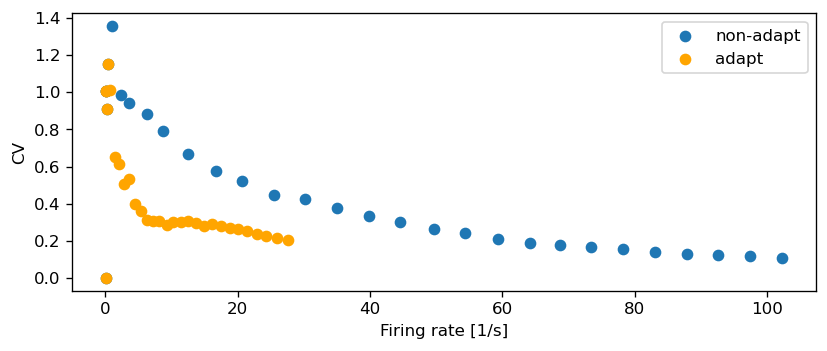
Task: What can you conclude about the behaviour of the adaptive neuron model on the basis of this diagram? In what ways is it qualitatively different from the non-adapting model?
Spike train autocorrelation
Autocorrelogram: histogram of time differences between (not necessarily adjacent) spikes.
[21]:
def spike_train_autocorrelation(spike_times, half_wind=50., plot=True):
"""
Parameters
----------
half_wind : float
Half the window size in milliseconds.
"""
times = []
for t1 in spike_times:
for t2 in spike_times:
times.append(t2 - t1)
count, bin_edges = np.histogram(times, bins=41, range=(-half_wind, half_wind))
count = np.array(count) / len(times)
bin_centers = (bin_edges[:-1] + bin_edges[1:]) / 2.
if plot:
fig, ax = plt.subplots()
#ax.bar(bin_centers, count, width=.8 * (bin_edges[1] - bin_edges[0]))
ax.plot(bin_centers, count, marker="o")
ax.set_xlabel("$\\Delta$t [ms]")
ax.grid()
return bin_edges, count
The spike autocorrelogram for a regularly spiking neuron should show peaks at the firing period, and multiples thereof:
[22]:
spike_times = np.arange(0., 1000., 20.)
_ = spike_train_autocorrelation(spike_times)
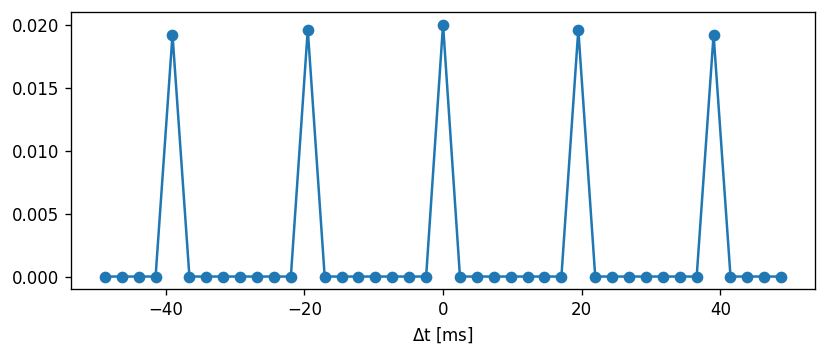
The spike autocorrelogram for a Poisson process should only show a peak around \(\Delta{}t\)=0 for any rate:
[23]:
spike_times = np.cumsum(np.random.exponential(10., 1000)) # cumsum turns ISIs into sequential spike times
_ = spike_train_autocorrelation(spike_times)
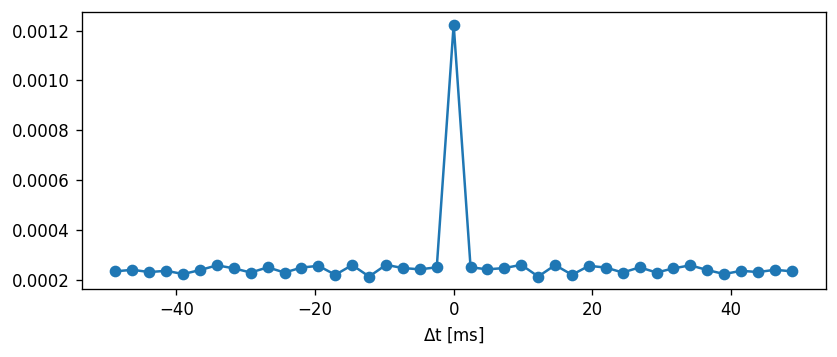
Task: Use the spike_train_autocorrelation() function to determine if neurons with and without adaptation are Poissonian in their response, when driven with a noisy input.
[25]:
def autocorr(spike_times):
ISI = np.diff(spike_times)
num = 0.
den = 0.
for i in range(len(ISI) - 1):
num += ISI[i] * ISI[i+1] - np.mean(ISI)**2
den += ISI[i]**2 - np.mean(ISI)**2
sum = num / den / (len(ISI) - 1)
return sum
N = 2
c = np.nan * np.ones(N)
rate = np.nan * np.ones(N)
mu = 500.
for i, dth in enumerate(np.linspace(0., 10., N)):
spike_times = evaluate_neuron(neuron_model_name_adapt_thresh_ou,
module_name=module_name_adapt_thresh_ou,
stimulus_type="Ornstein-Uhlenbeck",
mu=mu,
sigma=500.,
t_sim=2000.,
plot=False,
neuron_parms={"Delta_Theta" : dth,
"tau_Theta" : 100.})
_ = spike_train_autocorrelation(spike_times, half_wind=200.)
isi = np.diff(spike_times)
c[i] = np.std(isi) / np.mean(isi)#autocorr(spike_times)
times = []
for t1 in spike_times:
for t2 in spike_times:
times.append(t2 - t1)
rate[i] = len(spike_times) / 10.
Apr 19 11:19:52 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:19:52 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:19:52 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 2000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:19:52 SimulationManager::run [Info]:
Simulation finished.
Apr 19 11:19:52 Install [Info]:
loaded module nestml_db743385b3864e6e9f1eb9b781769b0e_module
Apr 19 11:19:52 NodeManager::prepare_nodes [Info]:
Preparing 3 nodes for simulation.
Apr 19 11:19:52 SimulationManager::start_updating_ [Info]:
Number of local nodes: 3
Simulation time (ms): 2000
Number of OpenMP threads: 1
Not using MPI
Apr 19 11:19:52 SimulationManager::run [Info]:
Simulation finished.
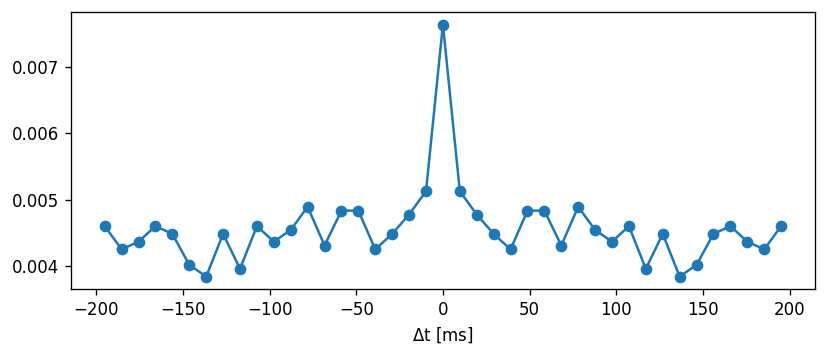
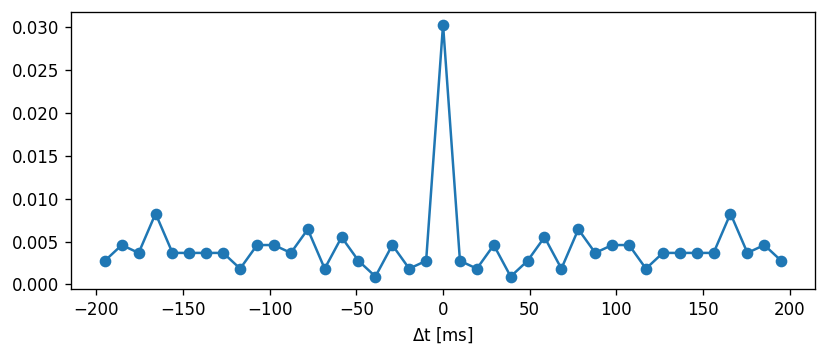
More characterisation
Meta task: How would you improve this tutorial? Extend it and share by submitting a pull request on https://github.com/nest/nestml/!
For more inspiration, try to reproduce the following figures:
Figure 5D from [2]
Autocorrelation: figure 8D from [3]
ISI correlation coefficient: figure 8B from [4]
Or try to see what the effect is of eliminating the membrane potential reset after spiking in the adaptive threshold model [2].
References
[1] Victor J. Barranca, Han Huang, and Sida Li. The impact of spike-frequency adaptation on balanced network dynamics. Cogn Neurodyn. 2019 Feb; 13(1): 105–120. https://doi.org/10.1007/s11571-018-9504-2
[2] Rony Azouz and Charles M. Gray. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. PNAS July 5, 2000 97 (14) 8110-8115; https://doi.org/10.1073/pnas.130200797
[3] Ryota Kobayashi & Katsunori Kitano. “Impact of slow K+ currents on spike generation can be described by an adaptive threshold model” Journal of Computational Neuroscience volume 40, pages 347–362 (2016) https://link.springer.com/article/10.1007/s10827-016-0601-0#Equ8