NESTML inhomogeneous Poisson generator tutorial

In this tutorial, we formulate a NESTML model for an inhomogeneous Poisson process [1], and simulate it in NEST Simulator.

The rate of the model is piecewise constant and is defined by an array containing desired rates (in units of 1/s) and an array of equal length containing the corresponding times (in units of ms). Please see the documentation for the NEST built-in inhomogeneous_poisson_generator for more details [2].

Preliminaries

The inhomogeneous Poisson model is defined in the file inhomogeneous_poisson.nestml. We call NESTML to generate and build the code, so the model can be instantiated in NEST Simulator.

[1]:

%matplotlib inline
import matplotlib.pyplot as plt
import nest
import numpy as np
from scipy.signal import convolve
import time
from pynestml.codegeneration.nest_code_generator_utils import NESTCodeGeneratorUtils

/home/charl/.local/lib/python3.11/site-packages/matplotlib/projections/__init__.py:63: UserWarning: Unable to import Axes3D. This may be due to multiple versions of Matplotlib being installed (e.g. as a system package and as a pip package). As a result, the 3D projection is not available.
  warnings.warn("Unable to import Axes3D. This may be due to multiple versions of "


              -- N E S T --
  Copyright (C) 2004 The NEST Initiative

 Version: 3.6.0-post0.dev0
 Built: Mar 26 2024 08:52:51

 This program is provided AS IS and comes with
 NO WARRANTY. See the file LICENSE for details.

 Problems or suggestions?
   Visit https://www.nest-simulator.org

 Type 'nest.help()' to find out more about NEST.

[2]:

# generate and build code
module_name, neuron_model_name = \
   NESTCodeGeneratorUtils.generate_code_for("inhomogeneous_poisson.nestml")


              -- N E S T --
  Copyright (C) 2004 The NEST Initiative

 Version: 3.5.0-rc1
 Built: Feb 21 2024 09:04:08

 This program is provided AS IS and comes with
 NO WARRANTY. See the file LICENSE for details.

 Problems or suggestions?
   Visit https://www.nest-simulator.org

 Type 'nest.help()' to find out more about NEST.

ANTLR runtime and generated code versions disagree: 4.13.1!=4.10.1
ANTLR runtime and generated code versions disagree: 4.13.1!=4.10.1
[12,inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml, WARNING, [1:0;26:0]]: Input block not defined!
[13,inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml, WARNING, [9:8;9:20]]: Variable 'N' has the same name as a physical unit!
[17,inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml, WARNING, [1:0;26:0]]: Input block not defined!
[18,inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml, WARNING, [9:8;9:20]]: Variable 'N' has the same name as a physical unit!
CMake Warning (dev) at CMakeLists.txt:93 (project):
  cmake_minimum_required() should be called prior to this top-level project()
  call.  Please see the cmake-commands(7) manual for usage documentation of
  both commands.
This warning is for project developers.  Use -Wno-dev to suppress it.

-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done

-------------------------------------------------------
nestml_09101de42ae44e479610c36e4cc709f5_module Configuration Summary
-------------------------------------------------------

C++ compiler         : /usr/bin/c++
Build static libs    : OFF
C++ compiler flags   :
NEST compiler flags  :  -std=c++11 -Wall -fopenmp -O2 -fdiagnostics-color=auto -g
NEST include dirs    :  -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli -fopenmp /usr/lib/x86_64-linux-gnu/libltdl.so  /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so

-------------------------------------------------------

You can now build and install 'nestml_09101de42ae44e479610c36e4cc709f5_module' using
  make
  make install

The library file libnestml_09101de42ae44e479610c36e4cc709f5_module.so will be installed to
  /tmp/nestml_target_11fovfgo
The module can be loaded into NEST using
  (nestml_09101de42ae44e479610c36e4cc709f5_module) Install       (in SLI)
  nest.Install(nestml_09101de42ae44e479610c36e4cc709f5_module)   (in PyNEST)

CMake Warning (dev) in CMakeLists.txt:
  No cmake_minimum_required command is present.  A line of code such as

    cmake_minimum_required(VERSION 3.26)

  should be added at the top of the file.  The version specified may be lower
  if you wish to support older CMake versions for this project.  For more
  information run "cmake --help-policy CMP0000".
This warning is for project developers.  Use -Wno-dev to suppress it.

-- Configuring done (0.1s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target
[ 66%] Building CXX object CMakeFiles/nestml_09101de42ae44e479610c36e4cc709f5_module_module.dir/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.o
[ 66%] Building CXX object CMakeFiles/nestml_09101de42ae44e479610c36e4cc709f5_module_module.dir/nestml_09101de42ae44e479610c36e4cc709f5_module.o
In file included from /home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp:43:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.h: In member function ‘virtual void inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml::set_status(const DictionaryDatum&)’:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.h:499:30: warning: comparison of integer expressions of different signedness: ‘std::vector<double>::size_type’ {aka ‘long unsigned int’} and ‘long int’ [-Wsign-compare]
  499 |   if ( tmp_rate_times.size() != tmp_N )
      |        ~~~~~~~~~~~~~~~~~~~~~~^~~~~~~~
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.h:513:31: warning: comparison of integer expressions of different signedness: ‘std::vector<double>::size_type’ {aka ‘long unsigned int’} and ‘long int’ [-Wsign-compare]
  513 |   if ( tmp_rate_values.size() != tmp_N )
      |        ~~~~~~~~~~~~~~~~~~~~~~~^~~~~~~~
In file included from /home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/nestml_09101de42ae44e479610c36e4cc709f5_module.cpp:47:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.h: In member function ‘virtual void inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml::set_status(const DictionaryDatum&)’:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.h:499:30: warning: comparison of integer expressions of different signedness: ‘std::vector<double>::size_type’ {aka ‘long unsigned int’} and ‘long int’ [-Wsign-compare]
  499 |   if ( tmp_rate_times.size() != tmp_N )
      |        ~~~~~~~~~~~~~~~~~~~~~~^~~~~~~~
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp: In member function ‘void inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp:150:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
  150 |   const double __resolution = nest::Time::get_resolution().get_ms();  // do not remove, this is necessary for the resolution() function
      |                ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp: In member function ‘void inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml::recompute_internal_variables(bool)’:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp:189:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
  189 |   const double __resolution = nest::Time::get_resolution().get_ms();  // do not remove, this is necessary for the resolution() function
      |                ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp: In member function ‘virtual void inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.cpp:220:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
  220 |     for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
      |                      ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-inhomogeneous_poisson/nestml/doc/tutorials/inhomogeneous_poisson/target/inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml.h:513:31: warning: comparison of integer expressions of different signedness: ‘std::vector<double>::size_type’ {aka ‘long unsigned int’} and ‘long int’ [-Wsign-compare]
  513 |   if ( tmp_rate_values.size() != tmp_N )
      |        ~~~~~~~~~~~~~~~~~~~~~~~^~~~~~~~
[100%] Linking CXX shared module nestml_09101de42ae44e479610c36e4cc709f5_module.so
[100%] Built target nestml_09101de42ae44e479610c36e4cc709f5_module_module
[100%] Built target nestml_09101de42ae44e479610c36e4cc709f5_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_11fovfgo/nestml_09101de42ae44e479610c36e4cc709f5_module.so

Feb 24 09:08:40 Install [Info]:
    loaded module nestml_09101de42ae44e479610c36e4cc709f5_module

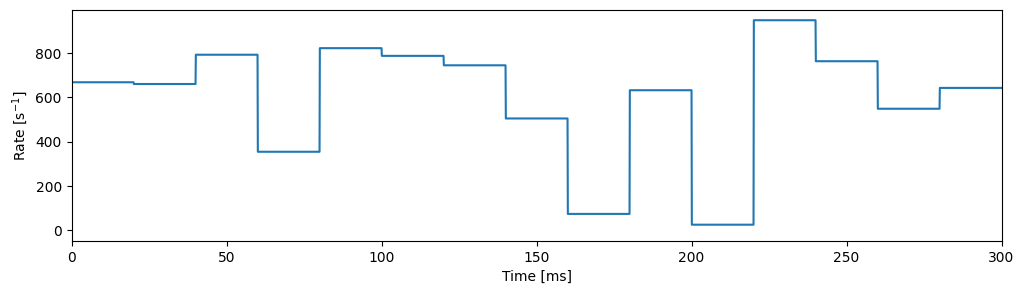
First, we generate a random piecewise constant target rate, that we want to feed into the Poisson generator model.

[3]:

def generate_input(num_steps, step_duration, resolution, distr_max, distr_min=0.):
    """
    Generates a piecewise constant input signal with amplitudes drawn from a uniform distribution

    Parameters
    ----------
    num_steps: int
        number of steps in the step function
    step_duration: int
        duration of each step in ms
    resolution: float
        resolution of the generated signal

    Returns
    -------
 The rate   ndarray
        continuous input signal (between distr_min and distr_max)
    ndarray
        time vector with all the times for which the signal is generated
    ndarray
        times at which signal amplitude shifts
    ndarray
        amplitudes
    """
    dist_range = [distr_min, distr_max]
    rand_distr = np.random.uniform(low=dist_range[0], high=dist_range[1], size=num_steps)
    rand_distr = rand_distr + abs(min(dist_range))
    inp_times = np.arange(resolution, num_steps * step_duration, step_duration)
    time_vec = np.arange(0, num_steps * step_duration + resolution, resolution)
    signal = np.zeros_like(time_vec)
    for tt in range(len(inp_times)):
        end_idx = int(round(inp_times[tt + 1] / resolution)) if tt + 1 < len(inp_times) else None
        signal[int(round(inp_times[tt] / resolution)):end_idx] = rand_distr[tt]

    return signal, time_vec, inp_times, rand_distr

[4]:

step_duration = 20.   # duration of each step [ms]
num_steps = 15        # number of unique input values
dt = .1               # simulation resolution [ms]

rate, times, inp_times, inp_amplitudes = generate_input(num_steps=num_steps,
                                                        step_duration=step_duration,
                                                        resolution=dt,
                                                        distr_max=1000.)

fig, ax = plt.subplots(figsize=(12, 3))
ax.plot(times, rate)
ax.set_xlim([0, num_steps * step_duration])
ax.set_xlabel("Time [ms]")
ax.set_ylabel("Rate [s${}^{-1}$]")

[4]:

Text(0, 0.5, 'Rate [s${}^{-1}$]')

../../_images/tutorials_inhomogeneous_poisson_inhomogeneous_poisson_6_1.png

Simulating the models

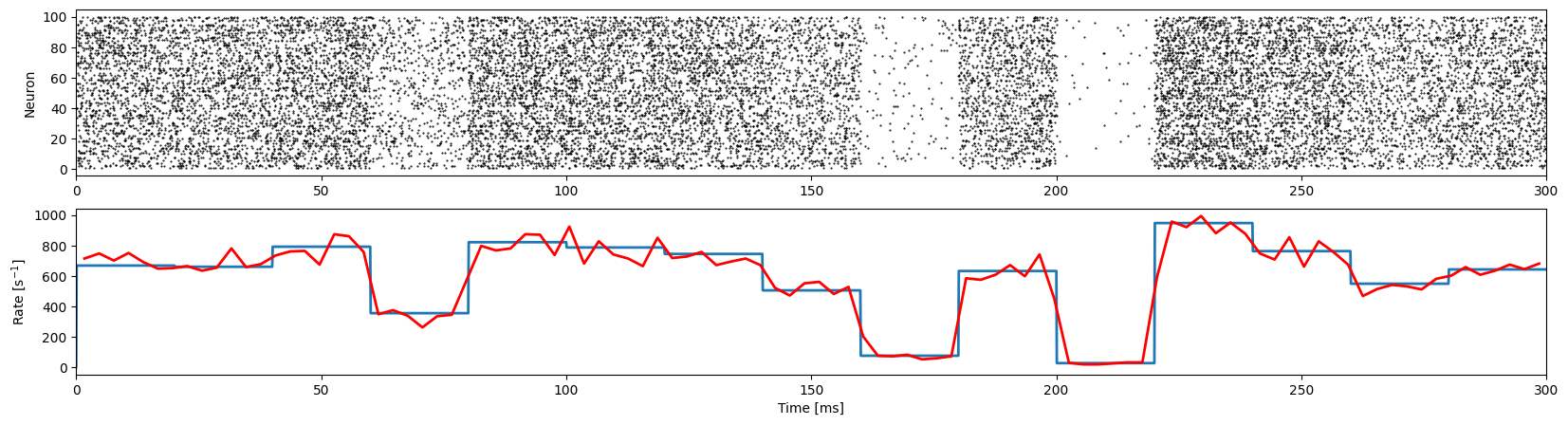
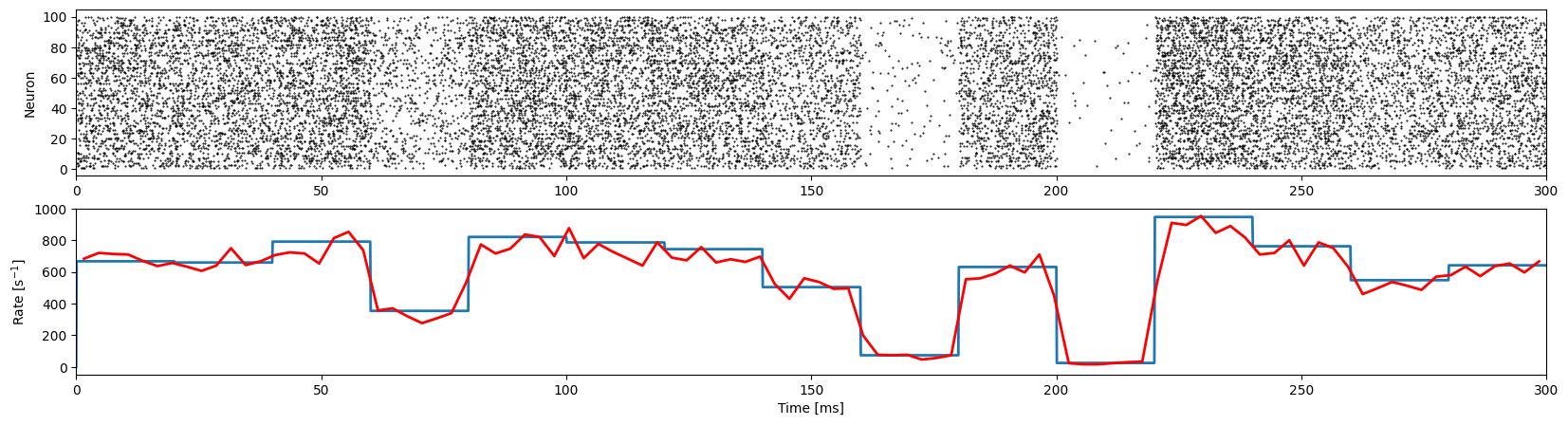
With the NESTML model loaded into the NEST kernel, we are ready to run the simulation. We define a helper function to run the simulation for each model: the NEST built-in inhomogeneous Poisson generator, and the one created in NESTML. We simulate n_instances (default: 100) of each model and compute the achieved average rate based on the simulation. The rates from the simulation (plotted below in red) should match the target rates (in blue). Events (spikes) emitted from each model are additionally plotted in a rastergram.

[5]:

def simulate_poisson_model(neuron_model, input_times, input_amplitudes, sig, n_instances=100, seed=1, dt=.1):
    sim_time = num_steps*step_duration

    np.random.seed(seed)
    nest.ResetKernel()
    nest.Install(module_name)
    nest.SetKernelStatus({'rng_seed': seed, 'resolution': dt, 'print_time': True})

    # create inhomogeneous poisson generator (time-dependent input signal)
    stim_pgen = nest.Create(neuron_model, n_instances)
    stim_pgen_params = {'rate_times': input_times, 'rate_values': input_amplitudes}
    if "N" in stim_pgen.get().keys():
        stim_pgen_params['N'] = len(input_times)
    nest.SetStatus(stim_pgen, params=stim_pgen_params)

    sr = nest.Create('spike_recorder')
    nest.Connect(stim_pgen, sr)

    nest.Simulate(sim_time)

    activity = nest.GetStatus(sr, 'events')[0]

    rate_estimated, rate_estimated_bin_edges = np.histogram(activity['times'], bins=100)
    rate_estimated_bin_centers = (rate_estimated_bin_edges[:-1] + rate_estimated_bin_edges[1:]) / 2
    bin_width = np.diff(rate_estimated_bin_centers)[0]
    rate = rate_estimated / bin_width
    rate /= n_instances
    rate *= 1E3

    # Plot
    fig = plt.figure(figsize=(20, 5))
    ax11 = fig.add_subplot(211)
    ax12 = fig.add_subplot(212, sharex=ax11)
    ax11.plot(activity['times'], activity['senders'], '.k', markersize=1)
    ax11.set_xlim([0., sim_time])
    ax11.set_ylabel("Neuron")

    ax12.plot(times, sig, linewidth=2)
    ax12.plot(rate_estimated_bin_centers, rate, linewidth=2, c='red')
    ax12.set_ylabel("Rate [s${}^{-1}$]")
    ax12.set_xlabel(r'Time [ms]')
    plt.show()

    return activity['times'], activity['senders']

NEST reference model

First, check that the NEST built-in inhomogeneous Poisson generator is working as expected.

[6]:

_ = simulate_poisson_model("inhomogeneous_poisson_generator", inp_times, inp_amplitudes, rate, dt=dt)


Feb 24 09:08:40 inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml [Warning]:
    Simulation resolution has changed. Internal state and parameters of the
    model have been reset!

Feb 24 09:08:40 SimulationManager::set_status [Info]:
    Temporal resolution changed from 0.1 to 0.1 ms.

Feb 24 09:08:40 NodeManager::prepare_nodes [Info]:
    Preparing 101 nodes for simulation.

Feb 24 09:08:40 SimulationManager::start_updating_ [Info]:
    Number of local nodes: 101
    Simulation time (ms): 300
    Number of OpenMP threads: 1
    Not using MPI

[ 100% ] Model time: 300.0 ms, Real-time factor: 0.0905

Feb 24 09:08:40 SimulationManager::run [Info]:
    Simulation finished.

../../_images/tutorials_inhomogeneous_poisson_inhomogeneous_poisson_10_1.png

NESTML model

Next, verify that the NESTML model is working correctly.

[7]:

_ = simulate_poisson_model(neuron_model_name, inp_times, inp_amplitudes, rate, dt=dt)


Feb 24 09:08:40 inhomogeneous_poisson09101de42ae44e479610c36e4cc709f5_nestml [Warning]:
    Simulation resolution has changed. Internal state and parameters of the
    model have been reset!

Feb 24 09:08:40 SimulationManager::set_status [Info]:
    Temporal resolution changed from 0.1 to 0.1 ms.

Feb 24 09:08:40 NodeManager::prepare_nodes [Info]:
    Preparing 101 nodes for simulation.

Feb 24 09:08:40 SimulationManager::start_updating_ [Info]:
    Number of local nodes: 101
    Simulation time (ms): 300
    Number of OpenMP threads: 1
    Not using MPI

[ 100% ] Model time: 300.0 ms, Real-time factor: 0.0372ms, Real-time factor: 0.0369

Feb 24 09:08:40 SimulationManager::run [Info]:
    Simulation finished.

../../_images/tutorials_inhomogeneous_poisson_inhomogeneous_poisson_12_1.png

References

[1] Wikipedia contributors. ‘Poisson Point Process.’ Wikipedia, The Free Encyclopedia. Accessed on February 23, 2024. https://en.wikipedia.org/wiki/Poisson_point_process.

[2] https://nest-simulator.readthedocs.io/en/stable/models/inhomogeneous_poisson_generator.html

Acknowledgements

This software was developed in part or in whole in the Human Brain Project, funded from the European Union’s Horizon 2020 Framework Programme for Research and Innovation under Specific Grant Agreements No. 720270, No. 785907 and No. 945539 (Human Brain Project SGA1, SGA2 and SGA3).

License

This notebook (and associated files) is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 2 of the License, or (at your option) any later version.

This notebook (and associated files) is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.