NESTML active dendrite tutorial
In this tutorial, we create a neuron model with a “nonlinear” or “active” dendritic compartment, that can, independently from the soma, generate a dendritic action potential. Instead of modeling the membrane potential of the dendritic compartment explicitly, the dendritic action potential (dAP) is modeled here as the injection of a rectangular (pulse shaped) dendritic current into the soma, parameterized by an amplitude and a duration. The rectangular shape can be interpreted as the approximation of an NMDA spike (Antic et al. 2010). A dendritic action potential is triggered when the total synaptic current exceeds a threshold.
The model is an adapted version of the neuron model introduced by Memmesheimer et al. (2012) and Jahnke et al. (2012), and has been used in (Bouhadjar et al., 2022).
Table of contents
[1]:
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import nest
import numpy as np
import os
from pynestml.codegeneration.nest_code_generator_utils import NESTCodeGeneratorUtils
# Set the verbosity in NEST to ERROR
nest.set_verbosity("M_ERROR")
/home/charl/.local/lib/python3.11/site-packages/matplotlib/projections/__init__.py:63: UserWarning: Unable to import Axes3D. This may be due to multiple versions of Matplotlib being installed (e.g. as a system package and as a pip package). As a result, the 3D projection is not available.
warnings.warn("Unable to import Axes3D. This may be due to multiple versions of "
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
Adding dAP current to the model
We will use a standard, linear integrate-and-fire neuron with the governing equation:
\begin{align} \frac{dV_m}{dt} &= -\frac{1}{\tau_m} (V_m - E_L) + \frac{1}{C_m} (I_{syn} + I_{dAP}) \end{align}
Here, the term \(I_{syn}\) contains all the currents flowing into the soma due to synaptic input, and \(I_{dAP}\) contains the contribution of a dendritic action potential.
Implementing the pulse shape
The dAP current is modeled here as a rectangular (pulse) function, parameterized by an amplitude (current strength) and width (duration).
parameters:
I_dAP_peak pA = 150 pA # current clamp value for I_dAP during a dendritic action potential
T_dAP ms = 10 ms # time window over which the dendritic current clamp is active
...
We also define a synaptic current threshold that, when crossed, initiates the dendritic action potential:
parameters:
I_th pA = 100 pA # current threshold for a dendritic action potential
...
The current is switched on and off as follows. When a dendritic action potential is triggered, the magnitude of the I_dAP current is set to I_dAP_peak, and a timer variable t_dAP is set to the duration of the current pulse, T_dAP. At each future run of the NESTML update block, the timer is decremented until it reaches 0, at which point the dendritic action potential current I_dAP is set back to zero.
update:
if t_dAP > 0 ms:
# during a dendritic action potential pulse
t_dAP -= resolution()
if t_dAP <= 0 ms:
# end of dendritic action potential
I_dAP = 0 pA
t_dAP = 0 ms
if I_syn > I_th:
# current-threshold, emit a dendritic action potential
t_dAP = T_dAP
I_dAP = I_dAP_peak
The complete neuron model is as follows:
[2]:
nestml_active_dend_model = '''
model iaf_psc_exp_active_dendrite_neuron:
state:
V_m mV = 0 mV # membrane potential
t_dAP ms = 0 ms # dendritic action potential timer
I_dAP pA = 0 pA # dendritic action potential current magnitude
equations:
# alpha shaped postsynaptic current kernel
kernel syn_kernel = (e / tau_syn) * t * exp(-t / tau_syn)
recordable inline I_syn pA = convolve(syn_kernel, spikes_in) * pA
V_m' = -(V_m - E_L) / tau_m + (I_syn + I_dAP + I_e) / C_m
parameters:
C_m pF = 250 pF # capacity of the membrane
tau_m ms = 20 ms # membrane time constant
tau_syn ms = 10 ms # time constant of synaptic current
V_th mV = 25 mV # action potential threshold
V_reset mV = 0 mV # reset voltage
I_e pA = 0 pA # external current
E_L mV = 0 mV # resting potential
# dendritic action potential
I_th pA = 100 pA # current threshold for a dendritic action potential
I_dAP_peak pA = 150 pA # current clamp value for I_dAP during a dendritic action potential
T_dAP ms = 10 ms # time window over which the dendritic current clamp is active
input:
spikes_in <- spike
output:
spike
update:
# solve ODEs
integrate_odes()
if t_dAP > 0 ms:
t_dAP -= resolution()
if t_dAP <= 0 ms:
# end of dendritic action potential
t_dAP = 0 ms
I_dAP = 0 pA
onCondition(I_syn > I_th):
# current-threshold, emit a dendritic action potential
t_dAP = T_dAP
I_dAP = I_dAP_peak
onCondition(V_m > V_th):
# emit somatic action potential
emit_spike()
V_m = V_reset
'''
Save to a temporary file and make the model available to instantiate in NEST (see Running NESTML):
[3]:
module_name, neuron_name = NESTCodeGeneratorUtils.generate_code_for(nestml_active_dend_model,
module_name="active_dend_module",
logging_level="ERROR") # try "INFO" or "DEBUG" for more debug information
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
CMake Warning (dev) at CMakeLists.txt:93 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
active_dend_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'active_dend_module' using
make
make install
The library file libactive_dend_module.so will be installed to
/tmp/nestml_target_gey6txpr
The module can be loaded into NEST using
(active_dend_module) Install (in SLI)
nest.Install(active_dend_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.6s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target
[ 33%] Building CXX object CMakeFiles/active_dend_module_module.dir/active_dend_module.o
[ 66%] Building CXX object CMakeFiles/active_dend_module_module.dir/iaf_psc_exp_active_dendrite_neuron_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_neuron_nestml.cpp: In member function ‘void iaf_psc_exp_active_dendrite_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_neuron_nestml.cpp:187:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
187 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_exp_active_dendrite_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_neuron_nestml.cpp:290:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
290 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_neuron_nestml.cpp:285:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
285 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
[100%] Linking CXX shared module active_dend_module.so
[100%] Built target active_dend_module_module
[100%] Built target active_dend_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_gey6txpr/active_dend_module.so
Running the simulation in NEST
Let’s define a function that will instantiate the active dendrite model, run a simulation, and plot and return the results.
[4]:
def evaluate_neuron(neuron_name, module_name, neuron_parms=None, t_sim=100., plot=True):
"""
Run a simulation in NEST for the specified neuron. Inject a stepwise
current and plot the membrane potential dynamics and action potentials generated.
Returns the number of postsynaptic action potentials that occurred.
"""
dt = .1 # [ms]
nest.ResetKernel()
try:
nest.Install(module_name)
except :
pass
neuron = nest.Create(neuron_name)
if neuron_parms:
for k, v in neuron_parms.items():
nest.SetStatus(neuron, k, v)
sg = nest.Create("spike_generator", params={"spike_times": [10., 20., 30., 40., 50.]})
multimeter = nest.Create("multimeter")
record_from_vars = ["V_m", "I_syn", "I_dAP"]
if "enable_I_syn" in neuron.get().keys():
record_from_vars += ["enable_I_syn"]
multimeter.set({"record_from": record_from_vars,
"interval": dt})
sr_pre = nest.Create("spike_recorder")
sr = nest.Create("spike_recorder")
nest.Connect(sg, neuron, syn_spec={"weight": 50., "delay": 1.})
nest.Connect(multimeter, neuron)
nest.Connect(sg, sr_pre)
nest.Connect(neuron, sr)
nest.Simulate(t_sim)
mm = nest.GetStatus(multimeter)[0]
timevec = mm.get("events")["times"]
I_syn_ts = mm.get("events")["I_syn"]
I_dAP_ts = mm.get("events")["I_dAP"]
ts_somatic_curr = I_syn_ts + I_dAP_ts
if "enable_I_syn" in mm.get("events").keys():
enable_I_syn = mm.get("events")["enable_I_syn"]
ts_somatic_curr = enable_I_syn * I_syn_ts + I_dAP_ts
ts_pre_sp = nest.GetStatus(sr_pre, keys='events')[0]['times']
ts_sp = nest.GetStatus(sr, keys='events')[0]['times']
n_post_spikes = len(ts_sp)
if plot:
n_subplots = 3
n_ticks = 4
if "enable_I_syn" in mm.get("events").keys():
n_subplots += 1
fig, ax = plt.subplots(n_subplots, 1, dpi=100)
ax[0].scatter(ts_pre_sp, np.zeros_like(ts_pre_sp), marker="d", c="orange", alpha=.8, zorder=99)
ax[0].plot(timevec, I_syn_ts, label=r"I_syn")
ax[0].set_ylabel("I_syn [pA]")
ax[0].set_ylim(0, np.round(1.1*np.amax(I_syn_ts)/50)*50)
ax[0].yaxis.set_major_locator(mpl.ticker.LinearLocator(n_ticks))
twin_ax = ax[0].twinx()
twin_ax.plot(timevec, I_dAP_ts, linestyle="--", label=r"I_dAP")
twin_ax.set_ylabel("I_dAP [pA]")
twin_ax.set_ylim(0, max(3, np.round(1.1*np.amax(I_dAP_ts)/50)*50))
twin_ax.legend(loc="upper right")
twin_ax.yaxis.set_major_locator(mpl.ticker.LinearLocator(n_ticks))
ax[-2].plot(timevec, ts_somatic_curr, label="total somatic\ncurrent")
ax[-2].set_ylabel("[pA]")
if "enable_I_syn" in mm.get("events").keys():
ax[1].plot(timevec, enable_I_syn, label="enable_I_syn")
ax[1].set_ylim([-.05, 1.05])
ax[1].set_yticks([0, 1])
ax[-1].plot(timevec, mm.get("events")["V_m"], label="V_m")
ax[-1].scatter(ts_sp, np.zeros_like(ts_sp), marker="d", c="olivedrab", alpha=.8, zorder=99)
ax[-1].set_ylabel("V_m [mV]")
ax[-1].set_xlabel("Time [ms]")
for _ax in set(ax) | set([twin_ax]):
_ax.grid()
if not _ax == twin_ax: _ax.legend(loc="upper left")
if not _ax == ax[-1]: _ax.set_xticklabels([])
for _loc in ['top', 'right', 'bottom', 'left']: _ax.spines[_loc].set_visible(False) # hide axis outline
for o in fig.findobj(): o.set_clip_on(False) # disable clipping
fig.show()
return n_post_spikes
[5]:
n_post_sp = evaluate_neuron(neuron_name, module_name,
neuron_parms={"I_th": 100., "I_dAP_peak": 400.})
assert n_post_sp == 2 # check for correctness of the result
/tmp/ipykernel_328427/1260340709.py:84: UserWarning:FigureCanvasAgg is non-interactive, and thus cannot be shown
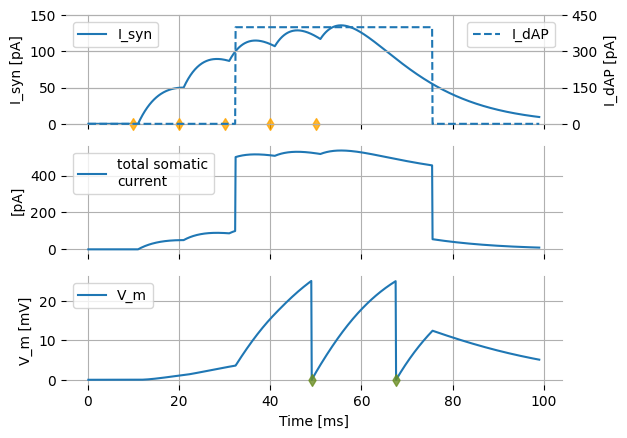
In the top panel, we can see the synaptic and dAP currents separately. Incoming action potentials from the presynaptic partner, triggering postsynaptic currents, are indicated by orange diamonds ♦. The middle panel shows the total synaptic current, which is equal to the sum of synaptic and dendritic action potential current. The bottom panel shows the resulting postsynaptic membrane potential, and postsynaptic (somatic) action potentials using green diamonds ♦.
The presynaptic action potentials by themselves are not sufficient by themselves to trigger a postsynaptic action potential, which can be seen by setting the dAP threshold to a very high value, preventing it from triggering. No postsynaptic spikes are observed.
[6]:
n_post_sp = evaluate_neuron(neuron_name, module_name,
neuron_parms={"I_th": 9999.})
assert n_post_sp == 0 # check for correctness of the result
/tmp/ipykernel_328427/1260340709.py:84: UserWarning:FigureCanvasAgg is non-interactive, and thus cannot be shown
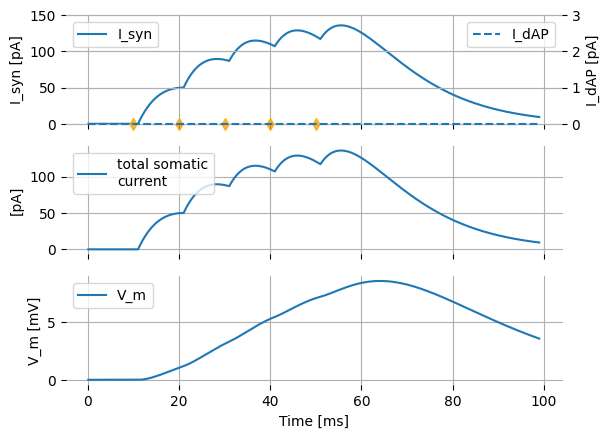
Dynamically controlling synaptic integration
We now add the additional requirement for the dendritic action potential to disable synaptic integration. When a dendritic action potential happens, we want to ignore synaptic currents for the duration of the action potential, and to reset the synaptic currents such that any presynaptic activity before the dendritic action potential is ignored.
To do this, we add a state variable enable_I_syn, that will have the value 1 if synaptic current integration is enabled, and 0 in case it is disabled. This variables multiplies the I_syn term in the differential equation for \(V_m\). The new governing equation is then:
\begin{align} \frac{dV_m}{dt} &= -\frac{1}{\tau_m} (V_m - E_L) + \frac{1}{C_m} (\mathtt{enable\_I\_syn} \cdot I_{syn} + I_{dAP}) \end{align}
We can then temporarily disable the synaptic current from contributing to the update of V_m by setting enable_I_syn to zero, for instance:
update:
if I_syn > I_th:
# current-threshold, emit a dendritic action potential
...
# temporarily pause synaptic integration
enable_I_syn = 0.
...
In order to ignore presynaptic input that arrives during and before a dendritic action potential, we use the inline aliasing feature of NESTML. Usually, synaptic integration is expressed as a convolution, for example:
equations:
kernel syn_kernel = exp(-t / tau_syn)
V_m' = -(V_m - E_L) / tau_m + convolve(syn_kernel, in_spikes) / C_m
...
We will define an inline expression that aliases this convolution (see https://nestml.readthedocs.io/en/latest/nestml_language.html#%28Re%29setting-synaptic-integration-state for a more detailed explanation):
equations:
inline I_syn pA = convolve(syn_kernel, in_spikes)
...
Now, we can not only use the variable I_syn in expressions, but we can also assign to it. To reset the state of synaptic integration (thereby “forgetting” any past action potential events):
update:
...
if t_dAP <= 0 ms:
# end of dendritic action potential
...
I_syn = 0 pA
I_syn' = 0 pA/ms
...
Putting it all together in a new model, we have:
[7]:
nestml_active_dend_reset_model = '''
model iaf_psc_exp_active_dendrite_resetting_neuron:
state:
V_m mV = 0 mV # membrane potential
t_dAP ms = 0 ms # dendritic action potential timer
I_dAP pA = 0 pA # dendritic action potential current magnitude
enable_I_syn real = 1. # set to 1 to allow synaptic currents to # <----
# contribute to V_m integration, 0 otherwise # <----
equations:
# alpha shaped postsynaptic current kernel
kernel syn_kernel = (e / tau_syn) * t * exp(-t / tau_syn)
recordable inline I_syn pA = convolve(syn_kernel, spikes_in) * pA
V_m' = -(V_m - E_L) / tau_m + (enable_I_syn * I_syn + I_dAP + I_e) / C_m
parameters:
C_m pF = 250 pF # capacity of the membrane
tau_m ms = 20 ms # membrane time constant
tau_syn ms = 10 ms # time constant of synaptic current
V_th mV = 25 mV # action potential threshold
V_reset mV = 0 mV # reset voltage
I_e pA = 0 pA # external current
E_L mV = 0 mV # resting potential
# dendritic action potential
I_th pA = 100 pA # current-threshold for a dendritic action potential
I_dAP_peak pA = 150 pA # current clamp value for I_dAP during a dendritic action potential
T_dAP ms = 10 ms # time window over which the dendritic current clamp is active
input:
spikes_in <- spike
output:
spike
update:
# solve ODEs
integrate_odes()
if t_dAP > 0 ms:
t_dAP -= resolution()
if t_dAP <= 0 ms:
# end of dendritic action potential
t_dAP = 0 ms
I_dAP = 0 pA
# reset and re-enable synaptic integration
I_syn = 0 pA # <----
I_syn' = 0 * s**-1 # <----
enable_I_syn = 1. # <----
onCondition(I_syn > I_th):
# current-threshold, emit a dendritic action potential
t_dAP = T_dAP
I_dAP = I_dAP_peak
# temporarily pause synaptic integration # <----
enable_I_syn = 0. # <----
onCondition(V_m > V_th):
# emit somatic action potential
emit_spike()
V_m = V_reset
'''
Save to a temporary file and make the model available to instantiate in NEST (see Running NESTML):
[8]:
module_name, neuron_name = NESTCodeGeneratorUtils.generate_code_for(nestml_active_dend_reset_model,
module_name="active_dend_reset_module",
logging_level="ERROR") # try "INFO" or "DEBUG" for more debug information
-- N E S T --
Copyright (C) 2004 The NEST Initiative
Version: 3.6.0-post0.dev0
Built: Mar 26 2024 08:52:51
This program is provided AS IS and comes with
NO WARRANTY. See the file LICENSE for details.
Problems or suggestions?
Visit https://www.nest-simulator.org
Type 'nest.help()' to find out more about NEST.
CMake Warning (dev) at CMakeLists.txt:93 (project):
cmake_minimum_required() should be called prior to this top-level project()
call. Please see the cmake-commands(7) manual for usage documentation of
both commands.
This warning is for project developers. Use -Wno-dev to suppress it.
-- The CXX compiler identification is GNU 12.3.0
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /usr/bin/c++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
-------------------------------------------------------
active_dend_reset_module Configuration Summary
-------------------------------------------------------
C++ compiler : /usr/bin/c++
Build static libs : OFF
C++ compiler flags :
NEST compiler flags : -std=c++17 -Wall -fopenmp -O2 -fdiagnostics-color=auto
NEST include dirs : -I/home/charl/julich/nest-simulator-install/include/nest -I/usr/include -I/usr/include -I/usr/include
NEST libraries flags : -L/home/charl/julich/nest-simulator-install/lib/nest -lnest -lsli /usr/lib/x86_64-linux-gnu/libltdl.so /usr/lib/x86_64-linux-gnu/libgsl.so /usr/lib/x86_64-linux-gnu/libgslcblas.so /usr/lib/gcc/x86_64-linux-gnu/12/libgomp.so /usr/lib/x86_64-linux-gnu/libpthread.a
-------------------------------------------------------
You can now build and install 'active_dend_reset_module' using
make
make install
The library file libactive_dend_reset_module.so will be installed to
/tmp/nestml_target_f0e0du76
The module can be loaded into NEST using
(active_dend_reset_module) Install (in SLI)
nest.Install(active_dend_reset_module) (in PyNEST)
CMake Warning (dev) in CMakeLists.txt:
No cmake_minimum_required command is present. A line of code such as
cmake_minimum_required(VERSION 3.26)
should be added at the top of the file. The version specified may be lower
if you wish to support older CMake versions for this project. For more
information run "cmake --help-policy CMP0000".
This warning is for project developers. Use -Wno-dev to suppress it.
-- Configuring done (0.5s)
-- Generating done (0.0s)
-- Build files have been written to: /home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target
[ 33%] Building CXX object CMakeFiles/active_dend_reset_module_module.dir/active_dend_reset_module.o
[ 66%] Building CXX object CMakeFiles/active_dend_reset_module_module.dir/iaf_psc_exp_active_dendrite_resetting_neuron_nestml.o
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_resetting_neuron_nestml.cpp: In member function ‘void iaf_psc_exp_active_dendrite_resetting_neuron_nestml::init_state_internal_()’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_resetting_neuron_nestml.cpp:189:16: warning: unused variable ‘__resolution’ [-Wunused-variable]
189 | const double __resolution = nest::Time::get_resolution().get_ms(); // do not remove, this is necessary for the resolution() function
| ^~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_resetting_neuron_nestml.cpp: In member function ‘virtual void iaf_psc_exp_active_dendrite_resetting_neuron_nestml::update(const nest::Time&, long int, long int)’:
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_resetting_neuron_nestml.cpp:298:24: warning: comparison of integer expressions of different signedness: ‘long int’ and ‘const size_t’ {aka ‘const long unsigned int’} [-Wsign-compare]
298 | for (long i = 0; i < NUM_SPIKE_RECEPTORS; ++i)
| ~~^~~~~~~~~~~~~~~~~~~~~
/home/charl/julich/nestml-fork-integrate_specific_odes/nestml/doc/tutorials/active_dendrite/target/iaf_psc_exp_active_dendrite_resetting_neuron_nestml.cpp:293:10: warning: variable ‘get_t’ set but not used [-Wunused-but-set-variable]
293 | auto get_t = [origin, lag](){ return nest::Time( nest::Time::step( origin.get_steps() + lag + 1) ).get_ms(); };
| ^~~~~
[100%] Linking CXX shared module active_dend_reset_module.so
[100%] Built target active_dend_reset_module_module
[100%] Built target active_dend_reset_module_module
Install the project...
-- Install configuration: ""
-- Installing: /tmp/nestml_target_f0e0du76/active_dend_reset_module.so
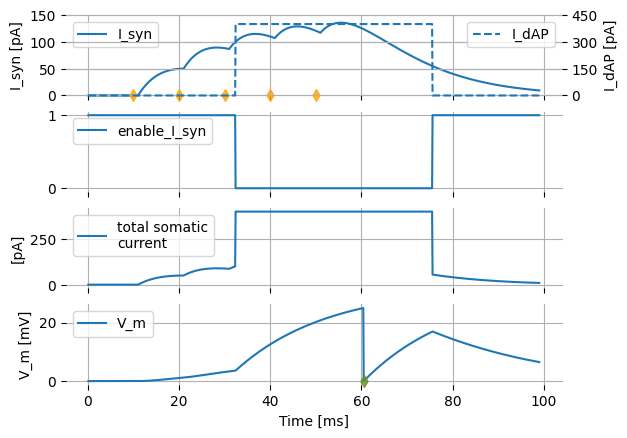
If we run the simulation with the same parameters as last time, we now observe only one instead of two action potentials, because the synaptic current (shown as I_syn in the top subplot below) does not contribute to V_m during the dendritic action potential interval.
[9]:
n_post_sp = evaluate_neuron(neuron_name, module_name,
neuron_parms={"I_th": 100., "I_dAP_peak": 400.})
assert n_post_sp == 1 # check for correctness of the result
/tmp/ipykernel_328427/1260340709.py:84: UserWarning:FigureCanvasAgg is non-interactive, and thus cannot be shown
Acknowledgements
We extend our gratitude to Younes Bouhadjar and Tom Tetzlaff for their contributions.
This software was developed in part or in whole in the Human Brain Project, funded from the European Union’s Horizon 2020 Framework Programme for Research and Innovation under Specific Grant Agreements No. 720270 and No. 785907 (Human Brain Project SGA1 and SGA2).
References
Jahnke, S., Timme, M. & Memmesheimer, R. M. (2012). Guiding synchrony through random networks. Physical Review X, 2(4), 041016. https://doi.org/10.1103/PhysRevX.2.041016
Memmesheimer, R. M. & Timme, M. (2012). Non-additive coupling enables propagation of synchronous spiking activity in purely random networks. PLoS Comput Biol, 8(4), e1002384. https://doi.org/10.1371/journal.pcbi.1002384
Antic, S.D. Zhou, W.-L., Moore, A.R., Short, S.M., & Ikonomu, K.D. (2010). The Decade of the Dendritic NMDA Spike. J Neurosci Res. Nov 1, 88(14). https://doi.org/10.1002/jnr.22444
Bouhadjar, Y., Wouters, D. J., Diesmann, M., & Tetzlaff, T. (2022). Sequence learning, prediction, and replay in networks of spiking neurons. PLoS Computational Biology, 18(6), e1010233.
Copyright
This file is part of NEST.
Copyright (C) 2004 The NEST Initiative
NEST is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 2 of the License, or (at your option) any later version.
NEST is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with NEST. If not, see http://www.gnu.org/licenses/.