iaf_psc_alpha

iaf_psc_alpha - Leaky integrate-and-fire neuron model

Description

iaf_psc_alpha is an implementation of a leaky integrate-and-fire model with alpha-function kernel synaptic currents. Thus, synaptic currents and the resulting post-synaptic potentials have a finite rise time.

The threshold crossing is followed by an absolute refractory period during which the membrane potential is clamped to the resting potential.

The general framework for the consistent formulation of systems with neuron like dynamics interacting by point events is described in [1]. A flow chart can be found in [2].

Critical tests for the formulation of the neuron model are the comparisons of simulation results for different computation step sizes.

The iaf_psc_alpha is the standard model used to check the consistency of the nest simulation kernel because it is at the same time complex enough to exhibit non-trivial dynamics and simple enough compute relevant measures analytically.

Note

If tau_m is very close to tau_syn_exc or tau_syn_inh, numerical problems may arise due to singularities in the propagator matrics. If this is the case, replace equal-valued parameters by a single parameter.

For details, please see IAF_neurons_singularity.ipynb in the NEST source code (docs/model_details).

References

[1]

Rotter S, Diesmann M (1999). Exact simulation of time-invariant linear systems with applications to neuronal modeling. Biologial Cybernetics 81:381-402. DOI: https://doi.org/10.1007/s004220050570

[2]

Diesmann M, Gewaltig M-O, Rotter S, & Aertsen A (2001). State space analysis of synchronous spiking in cortical neural networks. Neurocomputing 38-40:565-571. DOI: https://doi.org/10.1016/S0925-2312(01)00409-X

[3]

Morrison A, Straube S, Plesser H E, Diesmann M (2006). Exact subthreshold integration with continuous spike times in discrete time neural network simulations. Neural Computation, in press DOI: https://doi.org/10.1162/neco.2007.19.1.47

See also

iaf_psc_delta, iaf_psc_exp, iaf_cond_alpha

Parameters

Name	Physical unit	Default value	Description
C_m	pF	250pF	Capacitance of the membrane
tau_m	ms	10ms	Membrane time constant
tau_syn_inh	ms	2ms	Time constant of synaptic current
tau_syn_exc	ms	2ms	Time constant of synaptic current
refr_T	ms	2ms	Duration of refractory period
E_L	mV	-70mV	Resting potential
V_reset	mV	-70mV	Reset potential of the membrane
V_th	mV	-55mV	Spike threshold potential
I_e	pA	0pA	constant external input current

State variables

Name	Physical unit	Default value	Description
V_m	mV	E_L
refr_t	ms	0ms	Refractory period timer
is_refractory	boolean	false

Equations

\[\frac{ dV_{m} } { dt }= \frac{ -(V_{m} - E_{L}) } { \tau_{m} } + \frac{ I } { C_{m} }\]

Source code

The model source code can be found in the NESTML models repository here: iaf_psc_alpha.

Characterisation

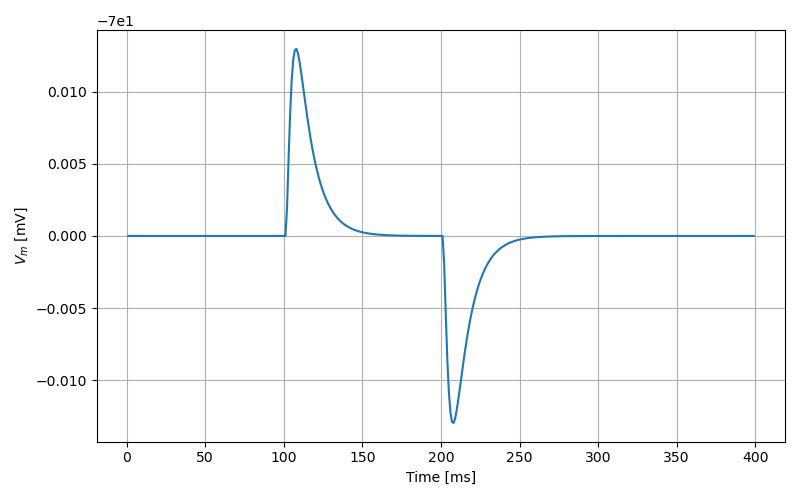
Synaptic response

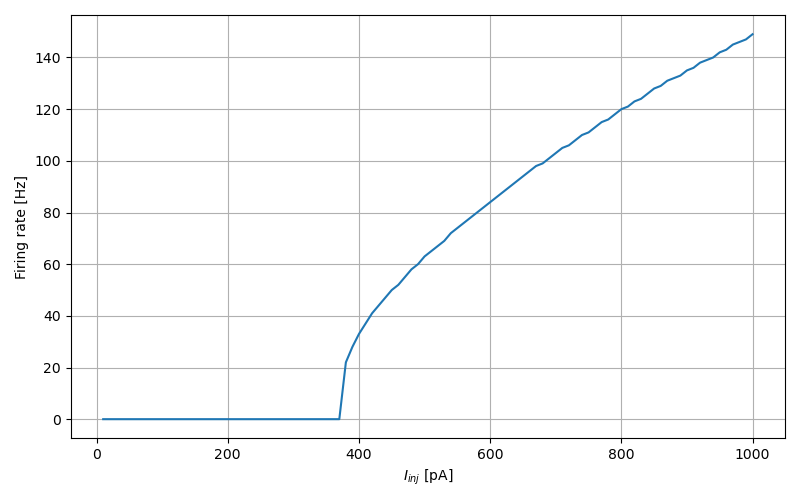
f-I curve