izhikevich

izhikevich - Izhikevich neuron model

Description

Implementation of the simple spiking neuron model introduced by Izhikevich [1]. The dynamics are given by:

\[\begin{split}dv/dt &= 0.04 v^2 + 5 v + 140 - u + I\\ du/dt &= a (b v - u)\end{split}\]

\[\begin{split}&\text{if}\;\; v \geq V_{th}:\\ &\;\;\;\; v \text{ is set to } c\\ &\;\;\;\; u \text{ is incremented by } d\\ & \, \\ &v \text{ jumps on each spike arrival by the weight of the spike}\end{split}\]

Incoming spikes cause an instantaneous jump in the membrane potential proportional to the strength of the synapse.

As published in [1], the numerics differs from the standard forward Euler technique in two ways:

1. the new value of \(u\) is calculated based on the new value of \(v\), rather than the previous value

2. the variable \(v\) is updated using a time step half the size of that used to update variable \(u\).

This model will instead be simulated using the numerical solver that is recommended by ODE-toolbox during code generation.

References

[1] (1,2)

Izhikevich, Simple Model of Spiking Neurons, IEEE Transactions on Neural Networks (2003) 14:1569-1572

Parameters

Name	Physical unit	Default value	Description
a	real	0.02	describes time scale of recovery variable
b	real	0.2	sensitivity of recovery variable
c	mV	-65mV	after-spike reset value of V_m
d	real	8.0	after-spike reset value of U_m
V_m_init	mV	-65mV	initial membrane potential
V_min	mV	-inf * mV	Absolute lower value for the membrane potential.
I_e	pA	0pA	constant external input current

State variables

Name	Physical unit	Default value	Description
V_m	mV	V_m_init	Membrane potential
U_m	real	b * V_m_init	Membrane potential recovery variable

Equations

\[\frac{ dV_{m} } { dt }= \frac 1 { \mathrm{ms} } \left( { (\frac{ 0.04 \cdot V_{m} \cdot V_{m} } { \mathrm{mV} } + 5.0 \cdot V_{m} + (140 - U_{m}) \cdot \mathrm{mV} + ((I_{e} + I_{stim}) \cdot \mathrm{GOhm})) } \right)\]

\[\frac{ dU_{m} } { dt }= \frac{ a \cdot (b \cdot V_{m} - U_{m} \cdot \mathrm{mV}) } { (\mathrm{mV} \cdot \mathrm{ms}) }\]

Source code

The model source code can be found in the NESTML models repository here: izhikevich.

Characterisation

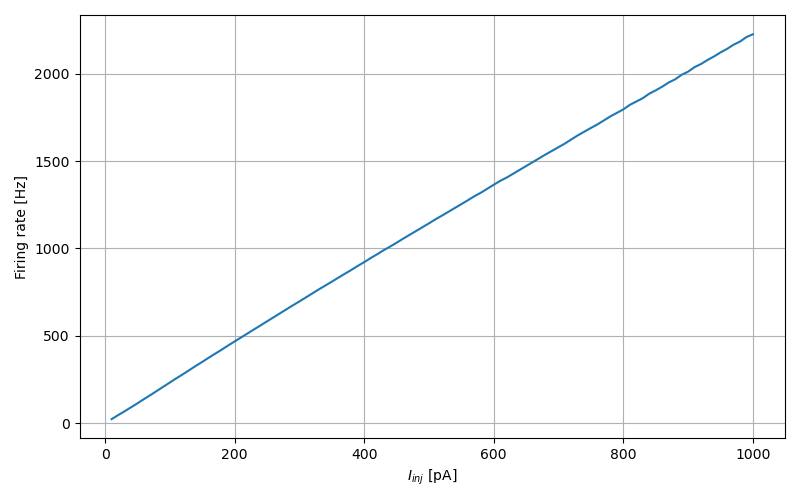
Synaptic response

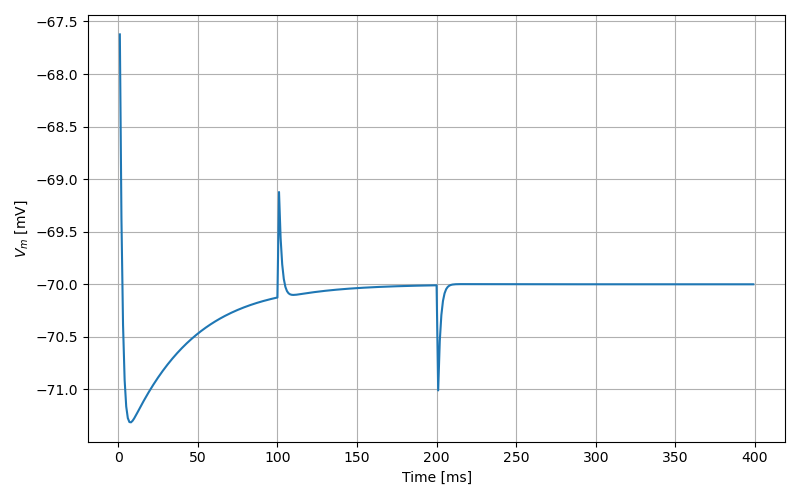
f-I curve