iaf_psc_delta

iaf_psc_delta - Current-based leaky integrate-and-fire neuron model with delta-kernel post-synaptic currents

Description

iaf_psc_delta is an implementation of a leaky integrate-and-fire model where the potential jumps on each spike arrival.

The threshold crossing is followed by an absolute refractory period during which the membrane potential is clamped to the resting potential.

Spikes arriving while the neuron is refractory, are discarded by default. If the property with_refr_input is set to true, such spikes are added to the membrane potential at the end of the refractory period, dampened according to the interval between arrival and end of refractoriness.

The general framework for the consistent formulation of systems with neuron like dynamics interacting by point events is described in [1]. A flow chart can be found in [2].

Critical tests for the formulation of the neuron model are the comparisons of simulation results for different computation step sizes. sli/testsuite/nest contains a number of such tests.

The iaf_psc_delta is the standard model used to check the consistency of the nest simulation kernel because it is at the same time complex enough to exhibit non-trivial dynamics and simple enough compute relevant measures analytically.

References

[1]

Rotter S, Diesmann M (1999). Exact simulation of time-invariant linear systems with applications to neuronal modeling. Biologial Cybernetics 81:381-402. DOI: https://doi.org/10.1007/s004220050570

[2]

Diesmann M, Gewaltig M-O, Rotter S, & Aertsen A (2001). State space analysis of synchronous spiking in cortical neural networks. Neurocomputing 38-40:565-571. DOI: https://doi.org/10.1016/S0925-2312(01)00409-X

See also

iaf_psc_alpha, iaf_psc_exp

Parameters

Name	Physical unit	Default value	Description
tau_m	ms	10ms	Membrane time constant
C_m	pF	250pF	Capacity of the membrane
refr_T	ms	2ms	Duration of refractory period
tau_syn	ms	2ms	Time constant of synaptic current
E_L	mV	-70mV	Resting membrane potential
V_reset	mV	-70mV	Reset potential of the membrane
V_th	mV	-55mV	Spike threshold
V_min	mV	-inf * 1mV	Absolute lower value for the membrane potential
I_e	pA	0pA	constant external input current

State variables

Name	Physical unit	Default value	Description
V_m	mV	E_L	Membrane potential
refr_t	ms	0ms	Refractory period timer
is_refractory	boolean	false

Equations

\[\frac{ dV_{m} } { dt }= \frac{ -(V_{m} - E_{L}) } { \tau_{m} } + \text{convolve}(K_{\delta}, spikes) \cdot (\frac{ \mathrm{mV} } { \mathrm{ms} }) + \frac 1 { C_{m} } \left( { (I_{e} + I_{stim}) } \right)\]

Source code

The model source code can be found in the NESTML models repository here: iaf_psc_delta.

Characterisation

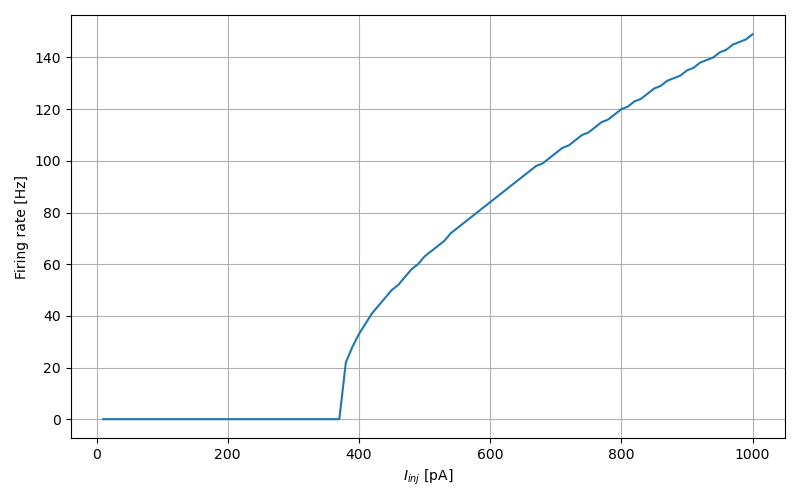
Synaptic response

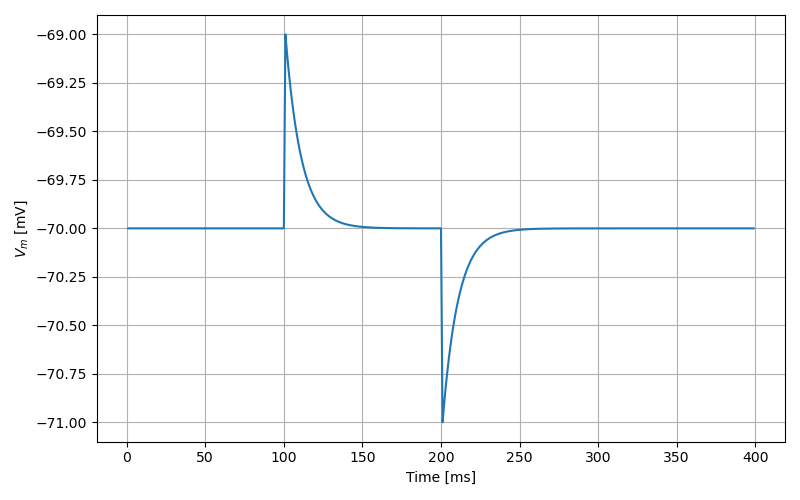
f-I curve