iaf_cond_alpha

iaf_cond_alpha - Simple conductance based leaky integrate-and-fire neuron model

Description

iaf_cond_alpha is an implementation of a spiking neuron using IAF dynamics with conductance-based synapses. Incoming spike events induce a post-synaptic change of conductance modelled by an alpha function. The alpha function is normalised such that an event of weight 1.0 results in a peak current of 1 nS at \(t = \tau_{syn}\).

References

[1]

Meffin H, Burkitt AN, Grayden DB (2004). An analytical model for the large, fluctuating synaptic conductance state typical of neocortical neurons in vivo. Journal of Computational Neuroscience, 16:159-175. DOI: https://doi.org/10.1023/B:JCNS.0000014108.03012.81

[2]

Bernander O, Douglas RJ, Martin KAC, Koch C (1991). Synaptic background activity influences spatiotemporal integration in single pyramidal cells. Proceedings of the National Academy of Science USA, 88(24):11569-11573. DOI: https://doi.org/10.1073/pnas.88.24.11569

[3]

Kuhn A, Rotter S (2004) Neuronal integration of synaptic input in the fluctuation- driven regime. Journal of Neuroscience, 24(10):2345-2356 DOI: https://doi.org/10.1523/JNEUROSCI.3349-03.2004

See also

iaf_cond_exp

Parameters

Name	Physical unit	Default value	Description
V_th	mV	-55mV	Threshold potential
V_reset	mV	-60mV	Reset potential
t_ref	ms	2ms	Refractory period
g_L	nS	16.6667nS	Leak conductance
C_m	pF	250pF	Membrane capacitance
E_exc	mV	0mV	Excitatory reversal potential
E_inh	mV	-85mV	Inhibitory reversal potential
E_L	mV	-70mV	Leak reversal potential (aka resting potential)
tau_syn_exc	ms	0.2ms	Synaptic time constant of excitatory synapse
tau_syn_inh	ms	2ms	Synaptic time constant of inhibitory synapse
I_e	pA	0pA	constant external input current

State variables

Name	Physical unit	Default value	Description
r	integer	0	counts number of tick during the refractory period
V_m	mV	E_L	membrane potential

Equations

\[\frac{ dV_{m} } { dt }= \frac 1 { C_{m} } \left( { (-I_{leak} - I_{syn,exc} - I_{syn,inh} + I_{e} + I_{stim}) } \right)\]

Source code

The model source code can be found in the NESTML models repository here: iaf_cond_alpha.

Characterisation

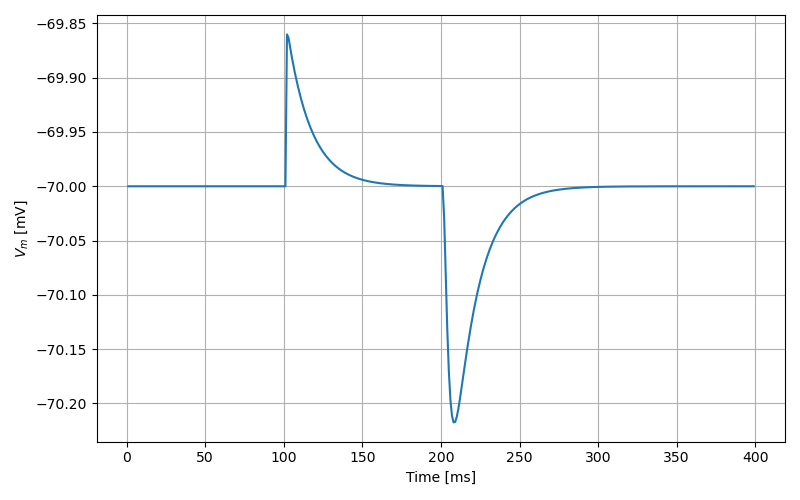
Synaptic response

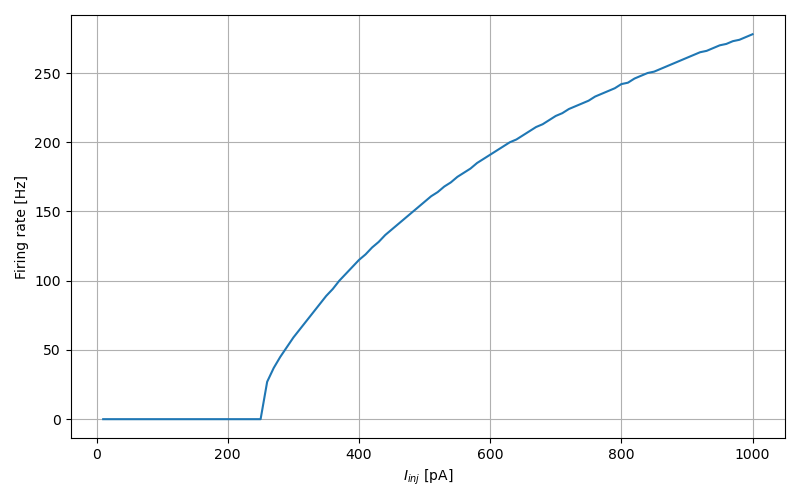
f-I curve