hh_psc_alpha

hh_psc_alpha - Hodgkin-Huxley neuron model

Description

hh_psc_alpha is an implementation of a spiking neuron using the Hodgkin-Huxley formalism.

Incoming spike events induce a post-synaptic change of current modelled by an alpha function. The alpha function is normalised such that an event of weight 1.0 results in a peak current of 1 pA.

Spike detection is done by a combined threshold-and-local-maximum search: if there is a local maximum above a certain threshold of the membrane potential, it is considered a spike.

Problems/Todo

• better spike detection

• initial wavelet/spike at simulation onset

References

[1]

Gerstner W, Kistler W (2002). Spiking neuron models: Single neurons, populations, plasticity. New York: Cambridge University Press

[2]

Dayan P, Abbott LF (2001). Theoretical neuroscience: Computational and mathematical modeling of neural systems. Cambridge, MA: MIT Press. https://pure.mpg.de/pubman/faces/ViewItemOverviewPage.jsp?itemId=item_3006127>

[3]

Hodgkin AL and Huxley A F (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology 117. DOI: https://doi.org/10.1113/jphysiol.1952.sp004764

See also

hh_cond_exp_traub

Parameters

Name	Physical unit	Default value	Description
V_m_init	mV	-65mV	Initial membrane potential
C_m	pF	100pF	Membrane Capacitance
g_Na	nS	12000nS	Sodium peak conductance
g_K	nS	3600nS	Potassium peak conductance
g_L	nS	30nS	Leak conductance
E_Na	mV	50mV	Sodium reversal potential
E_K	mV	-77mV	Potassium reversal potential
E_L	mV	-54.402mV	Leak reversal Potential (aka resting potential)
refr_T	ms	2ms	Duration of refractory period
tau_syn_exc	ms	0.2ms	Rise time of the excitatory synaptic alpha function
tau_syn_inh	ms	2ms	Rise time of the inhibitory synaptic alpha function
I_e	pA	0pA	constant external input current

State variables

Name	Physical unit	Default value	Description
V_m	mV	V_m_init	Membrane potential
V_m_old	mV	V_m_init	Membrane potential at previous timestep for threshold check
refr_t	ms	0ms	Refractory period timer
is_refractory	boolean	false
Act_m	real	alpha_m_init / (alpha_m_init + beta_m_init)	Activation variable m for Na
Inact_h	real	alpha_h_init / (alpha_h_init + beta_h_init)	Inactivation variable h for Na
Act_n	real	alpha_n_init / (alpha_n_init + beta_n_init)	Activation variable n for K

Equations

\[\frac{ dAct_{n} } { dt }= \frac 1 { \mathrm{ms} } \left( { (\alpha_{n} \cdot (1 - Act_{n}) - \beta_{n} \cdot Act_{n}) } \right)\]

\[\frac{ dAct_{m} } { dt }= \frac 1 { \mathrm{ms} } \left( { (\alpha_{m} \cdot (1 - Act_{m}) - \beta_{m} \cdot Act_{m}) } \right)\]

\[\frac{ dInact_{h} } { dt }= \frac 1 { \mathrm{ms} } \left( { (\alpha_{h} \cdot (1 - Inact_{h}) - \beta_{h} \cdot Inact_{h}) } \right)\]

\[\frac{ dV_{m} } { dt }= \frac 1 { C_{m} } \left( { (-(I_{Na} + I_{K} + I_{L}) + I_{e} + I_{stim} + I_{syn,exc} - I_{syn,inh}) } \right)\]

Source code

The model source code can be found in the NESTML models repository here: hh_psc_alpha.

Characterisation

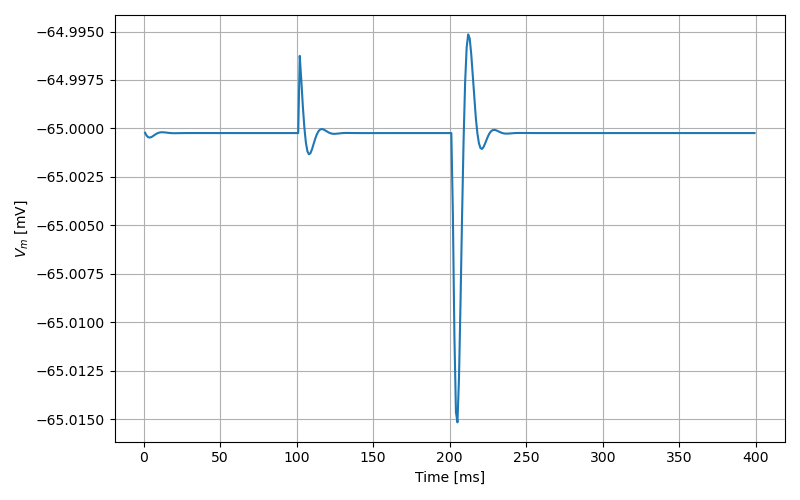
Synaptic response

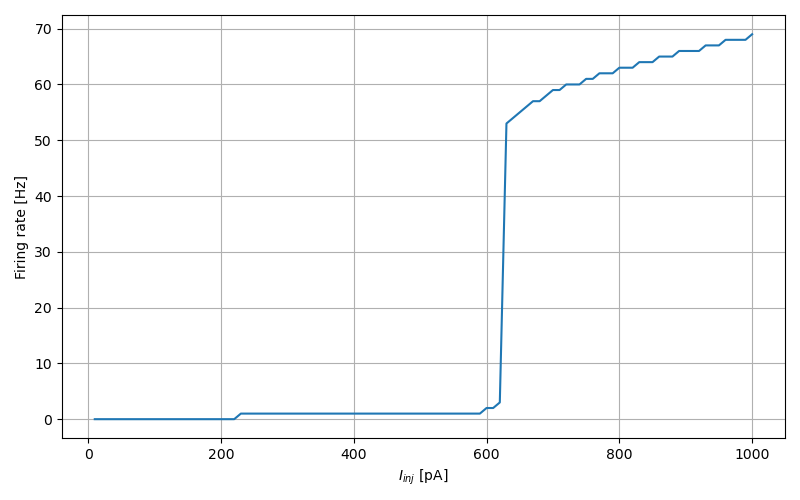
f-I curve